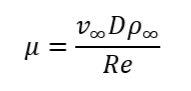В этой статье мы продолжаем знакомить вас с Физическим процессом Акустика (ссылка на Часть 1). На примере обтекания цилиндра при малых значениях числа Рейнольдса будут рассмотрены 2 режима расчета акустического давления: совместный с гидродинамическим и последовательный.
1. Постановка задачи
При обтекании неподвижных твердых тел постоянным потоком (или же при движении тел с постоянной скоростью) могут возникать звуковые колебания, хотя каких-либо причин для периодических возмущений в среде, на первый взгляд, нет. Тем не менее, гудение проводов, струн, снастей кораблей и самолетов, свист при обтекании углов и щелей и другие подобные явления свидетельствуют об обратном. Звуки такого происхождения называются «эоловыми тонами» по имени Эола – повелителя ветров в древнегреческой мифологии. В наиболее простой постановке задачу об исследовании эоловых тонов можно рассмотреть на примере обтекания цилиндра, что часто используется для валидации и кроссверификации вычислительных кодов [1, 2].
Рассмотрим обтекание цилиндра воздушным потоком с постоянной скоростью, соответствующей значению числа Маха M = 0,2, при значении числа Рейнольдса Re = 150, температуре 300 К и давлении 101325 Па. В этом случае реализуется ламинарный режим обтекания, и задача может быть рассчитана в двумерной постановке. Если плотность воздуха определять по закону идеального газа, то скорость звука зависит только от температуры и в нашем случае равна c = 347,8 м/с. Это дает значение скорости набегающего потока ν∞= 69,6 м/с. Значения ν∞ , Re, диаметра цилиндра D, а также плотности воздуха в невозмущенной среде ρ∞, которая составляет 1,17 кг/м3, для удобства можно задать в виде постоянных Пользовательских переменных. В этом случае не составит труда задать значение динамического коэффициента вязкости воздуха µ, соответствующее заданному значению числа Рейнольдса
Выберем значение диаметра цилиндра D = 0,01 м, тогда для сравнения с результатами работ [1, 2], расчетная область должна составлять 1 м по горизонтали и 2 м по вертикали. Частота схода вихрей, которая определяется следующим образом: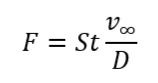
где St – число Струхаля, в общем случае зависящее от числа Рейнольдса. Для заданных параметров задачи воспользуемся формулой, полученной в работе [3]:
St = 0,2684 - 1,0356 * (Re)-1/2 = 0,184,
из которой получаем предварительную оценку частоты схода вихрей 1280 Гц.
Зная характерную частоту, можно оценить длину волны и размер ячейки, необходимый для достаточного разрешения волновой картины акустического поля.
Оценка длины акустической волны для первой гармоники λ = c / F ≈ 0,27 м. Если ограничиться первыми тремя гармониками, то минимальная длина волны будет составлять 0,09 м. Для приемлемого разрешения требуется не менее 25 ячеек на длину волны, таким образом, размер ячейки начальной сетки 0,002 м будет достаточным для решения поставленной акустической задачи. На рис. 1 представлено сечение начальной сетки в окрестности цилиндра.
Рис. 1 Начальная сетка в окрестности цилиндра.
Если предположить, что образующиеся вихри будут иметь характерный размер, равный диаметру цилиндра, то, очевидно, такого размера сетки недостаточно для их разрешения при гидродинамическом расчете. Таким образом, в области вихреобразования необходимо задать адаптацию. После предварительных расчетов было получено, что для достижения частоты схода вихрей, соответствующей результатам других авторов, необходимо задать адаптацию 3-го уровня в области вихреобразования. Сгенерированная сетка в окрестности цилиндра приведена на рис. 2.
Рис. 2. Расчётная сетка в окрестности цилиндра.
Поскольку сход вихрей представляет собой нестационарный процесс, то корректные результаты расчёта могут быть получены только при использовании шага по времени, соответствующего конвективному числу CFL = 1.
2. Гидродинамический расчёт
На первом этапе (0–0,01 с) был произведён предварительный гидродинамический расчёт, в котором была получена дорожка Кармана, представленная на рис. 3 в виде слоя Z-компоненты переменной «Завихренность». В области адаптации, которая обозначена прямоугольником, видно чередование вихрей, соответствующих положительным и отрицательным значениям компоненты завихренности.
Рис. 3. Дорожка Кармана.
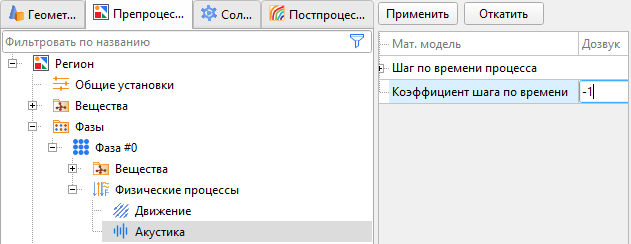
При запуске предварительного расчёта для возможности вычисления величин из физического процесса «Акустика» необходимо добавить этот процесс в фазу, при этом коэффициент шага по времени должен равняться −1 (рис. 4).
Рис. 4. Задание коэффициента шага по времени для физического процесса «Акустика».
Для количественной верификации гидродинамического расчёта рассмотрим коэффициенты подъёмной силы (cl) и силы сопротивления (cd), изменения которых можно пронаблюдать в окне «Пользовательские величины».
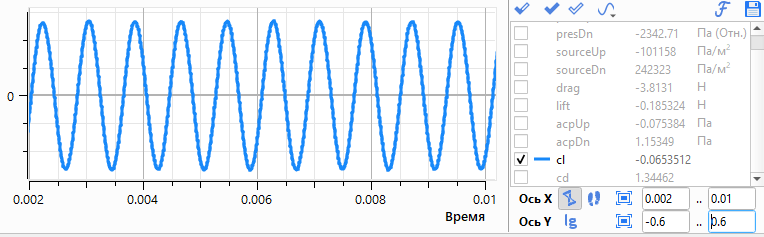
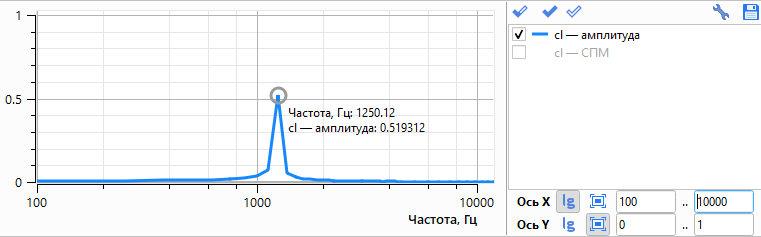
На рис. 5 представлена зависимость коэффициента подъёмной силы от времени и его спектр. Этот коэффициент изменяется периодически: каждый полупериод соответствует сходу вихря с верхней или нижней части цилиндра, т. е. частота соответствует частоте схода пары вихрей.
Рис. 5. Коэффициент подъёмной силы и его спектр.
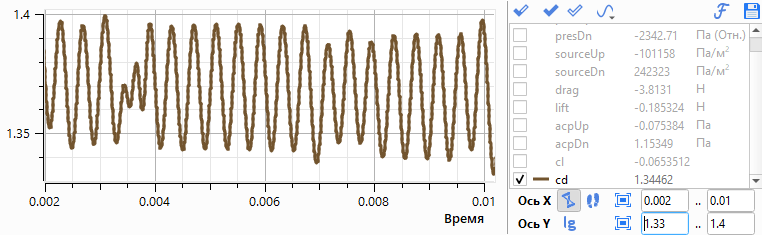
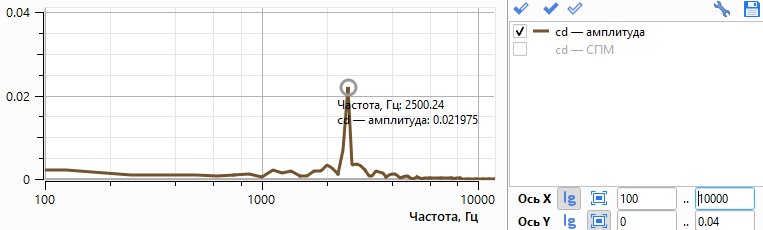
На рис. 6 представлена зависимость коэффициента силы сопротивления от времени и его спектр. Этот коэффициент также изменяется периодически, но в отличие от коэффициента подъёмной силы его частота в 2 раза выше, что соответствует сходу каждого вихря.
Рис. 6. Коэффициент силы сопротивления и его спектр.
В таблице 1 представлены значения измеренных величин и их сравнение с данными из обзора и результатов работы [2].
Таблица 1. Сравнение полученных результатов.
|
Источник данных |
cl |
cd |
St |
|
обзор из [2] |
1,279 - 1,363 |
0,167 - 0,389 |
0,18 – 0,19 |
|
результаты [2] |
1,332 |
0,365 |
0,182 |
|
FlowVision |
1,364 |
0,372 |
0,18 |
|
Отклонение, % |
2,4 |
2 |
1,1 |
Как видно из таблицы, отклонения значений коэффициентов сил и числа Струхаля, рассчитанных в FlowVision и в работе [2], не превышают 2,4 %.
Совместный расчёт гидродинамики и акустики
На втором этапе (0,01 – 0,02 с) был произведен совместный расчет гидродинамики и акустики.
В FlowVision реализованы два подхода для расчета с использованием физического процесса «Акустика»: одновременный с гидродинамическим расчетом и последовательный, когда во время расчета гидродинамики сохраняются данные для акустического источника, который используется в последующем акустическом расчете. В обоих случаях используются компактные источники (ограниченные выделенным параллелепипедом), что является отличительной особенностью FlowVision по сравнению с другими CFD комплексами.
При гидродинамическом расчете положение параллелепипеда для источника может быть определено с помощью слоя значений Дополнительной переменной «Интенсивность источника звука (осредненное)». Эта переменная появилась в новой версии 3.15.02 (именно для этого физический процесс «Акустика» должен быть подключен в Фазе, даже если не производится его расчет). В нашем случае осреднение было включено с 0,005 с. На рис. 7 представлен цветовой слой этой величины, красным выделен параллелепипед, охватывающий область ее максимальных значений. Выбор именно этой области (как видно на Рис. 7 есть еще варианты) обусловлен физическими соображениями. В работе [4] показано экспериментально, что образование вихревого звука связано с отсоединением вихрей в следе за телом, в области до образования стабильной дорожки Кармана.
Рис. 7 Слой осредненных значений переменной «Интенсивность источника звука». Красным выделен параллелепипед для источника звука.
В результате был выбран параллелепипед размером 0,015 м на 0,03 м с опорной точкой, расположенной на расстоянии 0,018 м от оси цилиндра по оси Х. Также заметим, что размер бокса по нерасчетной оси рекомендуется выбрать меньше толщины расчетной области, в данном случае выбрано 0,0098 м при толщине 0,01 м. Это необходимо для обеспечения нахождения точек расчета сохраняемых значений акустического источника в пределах расчётной области при решении задач в двумерной постановке.
После определения местоположения и размеров параллелепипеда источника, необходимо выполнить следующие операции:
1. Задать значение коэффициента шага по времени для физического процесса «Акустика» равное 1;
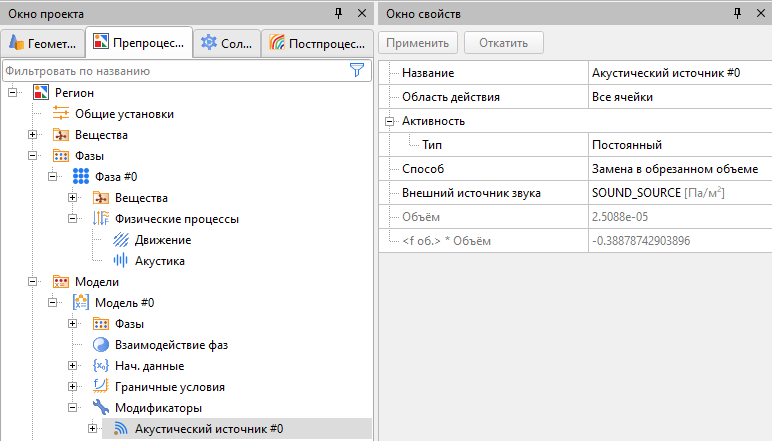
2. Создать модификатор «Акустический источник», в котором Внешний источник звука задан переменной «Гидродинамический источник звука» (рис. 8).
3. Задать постоянный шаг по времени для вычислений 1е-6 с. Такой выбор шага по времени позволяет рассчитывать акустическое давление за 5 - 6 итераций на каждом шаге расчета гидродинамики, поскольку схема расчета «Акустики» явная с постоянным шагом, соответствующим диффузионному CFL = 1 (в данном расчете 1,8е-7 с).
Рис. 8. Задание свойств модификатора «Акустический источник».
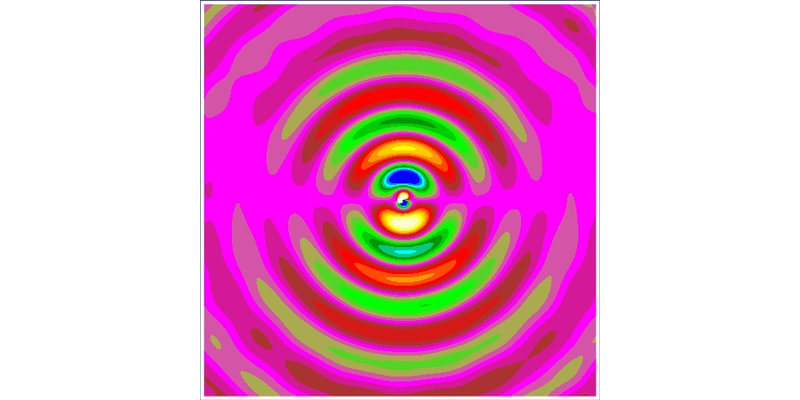
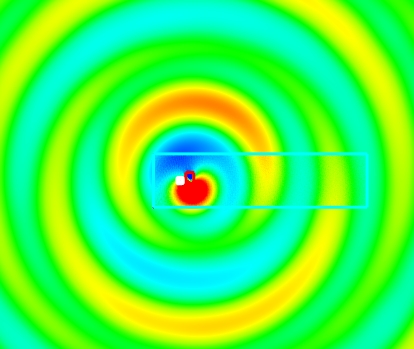
На рис. 9а представлен цветовой слой «Акустическое давление», полученный в конце расчёта. На рис. 9б показана область в окрестности цилиндра.
а
б
Рис. 9. Акустическое давление при совместном расчёте акустики и гидродинамики.
Как видно из рис. 9(б), в окрестности выделенного бокса источника картина поля имеет чётко выраженную дипольную структуру, которая размывается на расстояниях порядка половины длины акустической волны.
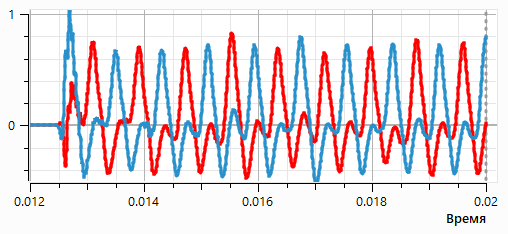
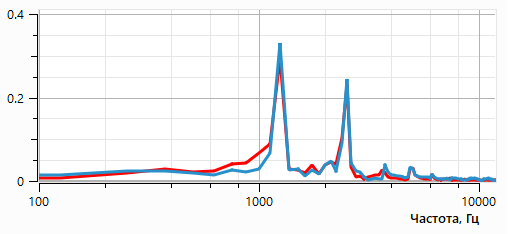
На рис. 10 представлены зависимости акустического давления от времени и его Фурье-спектры на датчиках (голубые точки на рис. 9а), расположенных на расстоянии 0,8 м от центра цилиндра, что примерно соответствует трём длинам акустической волны на основной частоте.
а 
б
Рис. 10. Акустическое давление от времени на датчиках (красный — верх, голубой — низ) (а), Фурье-спектр (б).
Как видно из рис. 10а, зависимости от времени акустического давления для верхнего и нижнего датчиков имеют сдвиг фазы, приблизительно равный половине периода, что соответствует дипольному характеру излучения. Спектры сигналов (рис. 10б) содержат помимо основной частоты (1250 Гц) ярко выраженную вторую гармонику (2500 Гц), что и вызывает отклонения от канонической картины поля дипольного излучения.
Заметим, что при задании параметров начальной сетки предполагалось наличие трёх гармоник, так что приемлемый результат мог быть получен и на более грубой начальной сетке. Значение основной частоты соответствует значению St = 0,18, а среднеквадратичное значение акустического давления равно 0,772 Па. При нормировке на произведение плотности и квадрата скорости звука получается значение 5,44e-6, что на порядок меньше значения 7,76e-5, полученного в работе [2] на таком же расстоянии от центра цилиндра. Это объясняется разностью подходов к вычислению акустического давления. Использованный в [2] метод FWH даёт завышенные значения.
3. Расчёт акустики с модификатором «Гидродинамический источник звука»
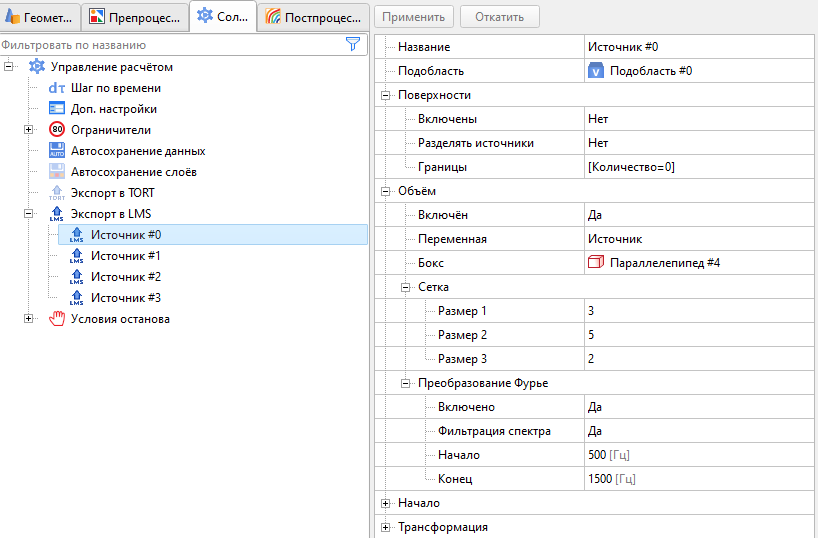
В течение совместного расчёта гидродинамики и акустики в FlowVision имеется возможность накопления и сохранения значения гидродинамического источника в выделенном боксе и в выделенном интервале частот с помощью экспорта в LMS (рис. 11). Для её демонстрации рассмотрим сохранение источника для первой гармоники частоты схода вихрей. Накопление производилось в течение всего совместного расчёта.
Как уже отмечено выше, бокс для накопления источника должен полностью находиться внутри расчётной области для корректного получения данных из расчётных ячеек. Сетка бокса источника должна быть достаточно мелкой для отражения особенностей поля в боксе. С другой стороны, необходимо иметь в виду, что сетка для акустического расчёта будет крупнее, и при совмещении сеток бокса источника и расчётной сетки для «Акустики» может потребоваться дополнительная адаптация, что повлечёт уменьшение шага по времени.
Рис. 11. Настройка экспорта в LMS.
Как уже отмечалось выше, оценка длины акустической волны λ = 0,27 м, тогда размер ячейки для акустического расчёта должен быть не более 0,01 м. Поскольку размер параллелепипеда 0,015 м на 0,03 м, то сетка 3 x 5 даст размер ячейки 0,005 м.
Для акустического расчёта предпочтительнее создать новый проект. Для получения диаграммы направленности будем использовать расчётную область 2 м × 2 м с размером ячеек 0,01 м. Для эффективного использования источника на его параллелепипеде зададим адаптацию первого уровня — в этом случае ячейки источника и сетки будут совпадать.
Также стоит отметить, что расчёт ведётся с шагом по времени, заданным диффузионным числом CFL = 1, что для данной сетки соответствует 3,6e-6 с. Заметим, что использование расчётной сетки с размером ячеек 0,005 м (что соответствует четырёхкратному увеличению количества элементов сетки) даст такой же результат.
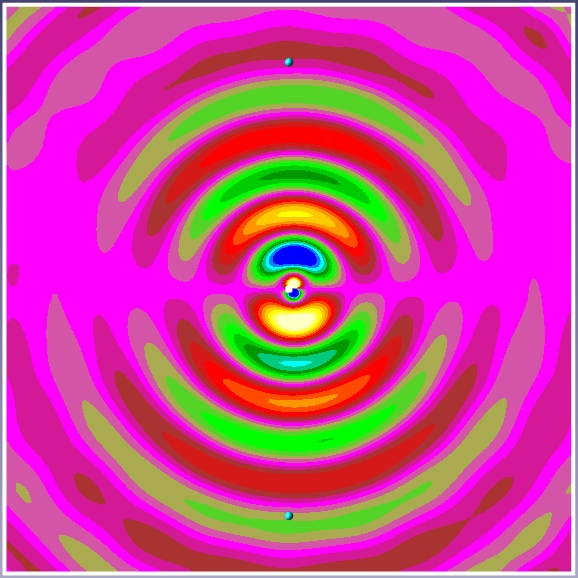
На рис. 12 представлен цветовой слой переменной «Акустическое давление», полученный в результате расчета и использованием Источника 0 (рис. 11). Видно, что поле Акустического давления имеет четко выраженную дипольную структуру, поскольку при сохранении источника были отфильтрованы высшие гармоники.
Рис. 12. Акустическое давление при расчете с использованием Источника 0 (рис. 11).
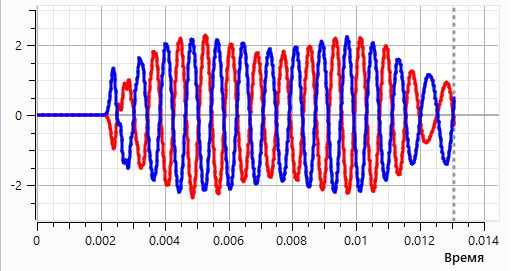
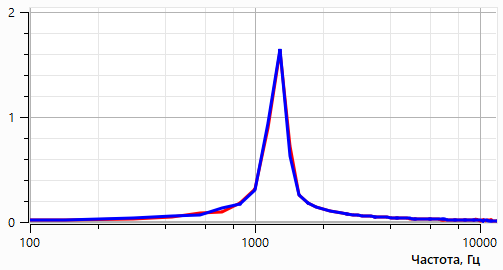
На рис. 13 представлены зависимости акустического давления от времени (а) и его Фурье спектры (б) на датчиках, расположенных на расстоянии 0,8 м от оси цилиндра, что примерно соответствует трем длинам акустической волны.
а
б
Рис. 13. Акустическое давление от времени на датчиках (0.7м от центра расчетной области, красный – верх, синий - низ) (а), Фурье-спектр (б).
По сравнению с рис. 10 на рис. 13 видно наличие только одной гармоники, что очевидно после использования фильтрации. Расчет среднеквадратичного значения акустического давления дает значение 9,6e-6 Па, что почти в 2 раза выше значения, полученного при совместном расчете. Различие объясняется отсутствием интерференции гармоник.
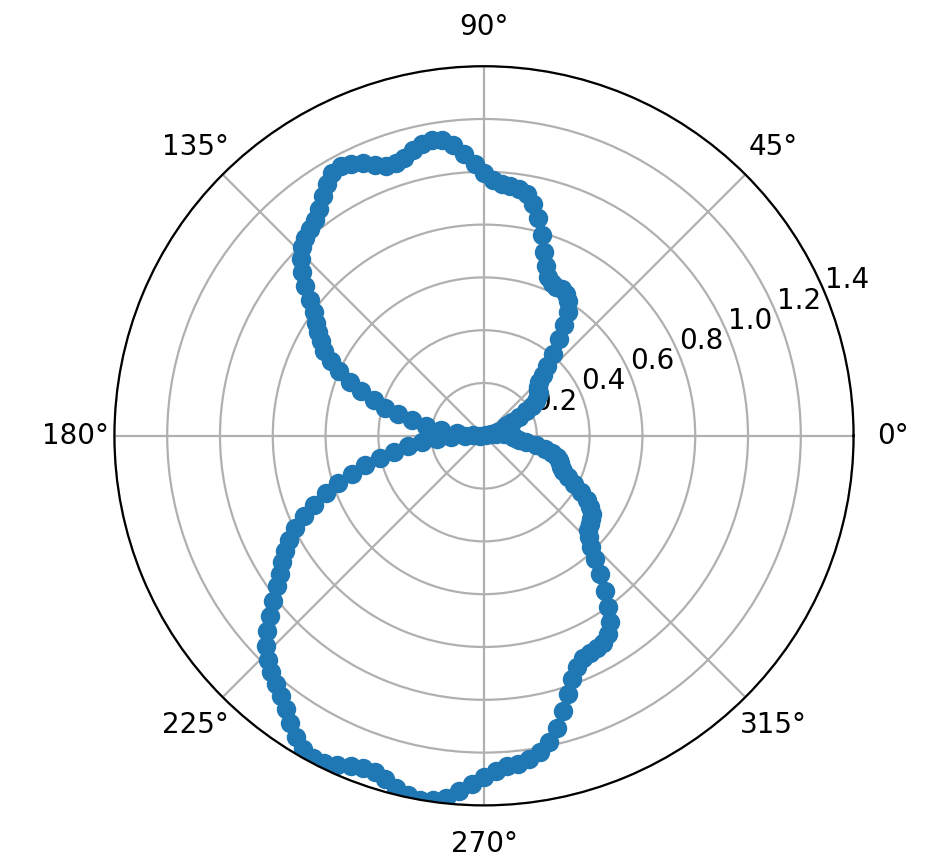
Дипольный характер излучения можно также продемонстрировать с помощью диаграммы направленности акустического излучения, которая представлена на рис. 14. Для ее построения необходимо в Постпроцессоре построить слой График вдоль эллипса, записать данные в файл, а далее построить круговую диаграмму в стороннем пакете.
Рис. 14. Диаграмма направленности акустического излучения на расстоянии 0,8 м от оси цилиндра, окружности соответствуют абсолютным значениям акустического давления в Па.
Заключение
В данной статье описаны основные подходы к расчетам акустических волн, возникающих при обтекании цилиндра при малых значения числа Рейнольдса в двумерной постановке. Проведена кроссверификация гидродинамического расчета на основе сравнения значений коэффициентов подъемной силы и силы сопротивления со значениями из работ [1, 2]. Значения акустического давления получились меньшими, чем в работе [2], что объясняется отличием методов расчета. Примеры подготовлены с использованием FlowVision версии 3.15.02. Более подробная информация по настройкам проектов приведена в учебном примере.
Если у вас возникли какие-либо вопросы по поводу содержания и материалов, пишите нам в Техническую поддержку.
Литература
[1] Inoue, O. and Hatakeyama, N., 2002. Sound generation by a two-dimensional circular cylinder in a uniform flow. Journal of Fluid Mechanics, 471, pp.285-314.
[2] Wang, X., Bhushan, S., Sescu, A., Luke, E., Manshoor, B. and Hattori, Y., 2024. Assessment of Turbulence Models for Cylinder Flow Aeroacoustics. Aerospace, 11(9), p.707.
[3] Fey, U., König, M. and Eckelmann, H., 1998. A new Strouhal–Reynolds-number relationship for the circular cylinder in the range 47< Re< 2×105. Physics of Fluids, 10(7), pp.1547-1549.
[4] Баженова, Л.А., Семёнов, А.Г., 2014. О природе источника вихревого звука при обтекании потоком цилиндрического профиля. Акустический журнал, 60(6), pp.645-645.