Рассматривается проблема численного моделирования процессов тепломассопереноса в реакторах на быстрых нейтронах с натриевым теплоносителем с помощью коммерческих Computational Fluid Dynamics (CFD) программных комплексов. Показано, что используемая в большинстве моделей турбулентности аналогия Рейнольдса не позволяет учитывать особенности теплопереноса в жидкометаллическом теплоносителе. Представлены результаты по разработке модели турбулентного теплопереноса LMS (Liquid Metal Sodium), учитывающей специфику натриевого теплоносителя. Это удалось сделать за счёт включения в систему уравнений модели выражения для турбулентного числа Прандтля, введения поправки, учитывающей гравитационную анизотропию турбулентного теплового потока, и тепловой пристеночной функции.
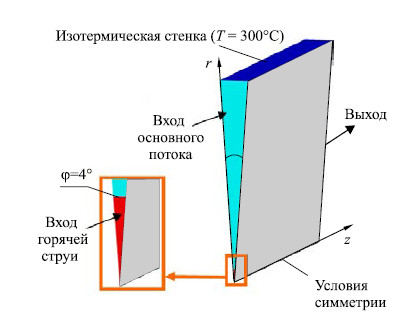
Модель реализована в CFD коде FlowVision, совместима с k−ε моделями турбулентности, и может применяться как в высокорейнольдсовых (с пристеночными функциями), так и в низкорейнольдсовых (без пристеночных функций) расчётах течения натрия. Выполнена верификация модели LMS на основе данных, полученных на стенде TEFLU (Карлсруэ, Германия), предназначенном для экспериментального моделирования процессов перемешивания разнотемпературных потоков натриевого теплоносителя. Опытным путём исследовано три режима течения: со свободной конвекцией, переходный и с вынужденной конвекцией. Для этих режимов представлены результаты численного моделирования, полученные посредством коммерческих CFD программных комплексов ANSYS CFX, Star-CD, Fluent, FlowVision с моделью LMS и без неё. Показано, что результаты, полученные в программном комплексе FlowVision с моделью LMS, лучше согласуются с экспериментальными данными, чем результаты, полученные в других программных комплексах.
Публикация в журнале "Вычислительная механика сплошных сред" - 2014, т. 7, №3, с. 306-316 - "Разработка модели турбулентного теплопереноса для жидкометаллического натриевого теплоносителя и её верификация", Рогожкин С.А., Осипов С.Л., Фадеев И.Д., Шепелев С.Ф. (ОАО "ОКБМ Африкантов", Нижний Новгород, Россия), Аксенов А.А., Жлуктов С.В,, Сазонова М.Л., Шмелев В.В., скачать PDF - файл, 1062 КБ