Сегодня речь пойдёт о том, как сэкономить расчётную сетку в двухмерной задаче: секторной или плоской. Вообще, FlowVision - это трехмерный пакет. Но если в одном из направлений существует только одна расчетная ячейка, получается двухмерный расчет. Но двумерность пропадает при включении адаптации. Наш пользователь из ИВТАН придумал, как даже в этом случае вернуться к двумерности и существенно сэкономить расчетную сетку.
Неравномерная сетка и адаптация
Измельчить сетку у профиля обтекаемого объекта во FlowVision можно двумя способами:
- Используя сгущение начальной сетки (неравномерная начальная сетка)
Размер грани кубической ячейки около профиля - 0,0025 м;
Начальная сетка - 198 х 178 х 1 ячеек;
Количество ячеек расчётной сетки - 34 628. - Используя Адаптацию, например, по поверхности
Размер грани кубической ячейки 3 уровня адаптации - 0,0025 м;
Начальная сетка - 64 х 60 х 1 ячеек;
Количество ячеек расчётной сетки - 16 580.
Применение адаптации позволило уменьшить количество расчётных ячеек в 2 раза при том же размере ячеек у поверхности профиля!
Но мы ушли от 2D постановки задачи: после применения адаптации по толщине расчётной области уже не одна ячейка.
Адаптация во FlowVision всегда трёхмерная
Адаптация - это трёхмерное разделения ячейки на 8 одинаковых частей.
Что происходит при включении адаптации уровня n? Ячейка, заданная по толщине расчётной области, разделяется на 2n ячеек. Поэтому размерность задачи растёт несколько быстрее, чем хотелось бы для двухмерных расчетов.
Но есть способ сделать так, чтобы несмотря на адаптацию, по толщине всегда оставалась только одна ячейка в любом месте расчётной области. То есть при помощи некоторых доработок проекта можно будет свести трёхмерную адаптацию к двумерной.
Используйте нерасчетную подобласть на удалении от расчетной
Опишем алгоритм по шагам на примере задачи обтекания профиля NACA из учебника FlowVision.
Для начала откроем проект и сразу запустим его на расчёт. В окне мониторинга увидим количество расчётных ячеек - 588 496. Обратите внимание, что количество ячеек начальной сетки в направлении Z=1, а при запуске на расчёт оно возрастает до 8. Это происходит потому что в проекте включена адаптация, и ячейки адаптируются по всем направлениям.
А теперь мы продемонстрируем, как уменьшить количество ячеек. Следите за руками!
Шаг 1
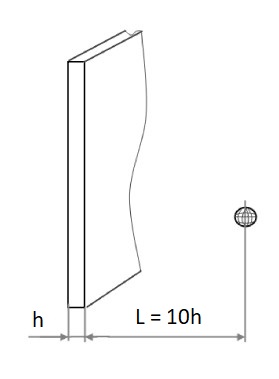
Создаем объект (например, сферу) и располагаем его на отдалении от плоскости расчёта. Величину этого отдаления вычислим по формуле: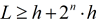 
, где n - максимальный уровень адаптации, заданный в проекте.
Шаг 2
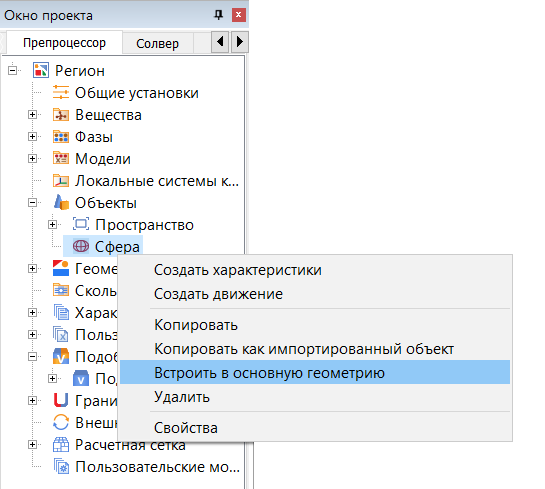
В контекстном меню созданной сферы выбираем "Встроить в основную геометрию".
В результате этого действия появится новая Подобласть. Мы не задаём в ней Модель - тогда подобласть останется нерасчётной и будет служить лишь для того, чтобы начальная сетка стала длиннее в направлении перпендикулярном плоскости расчёта.
Шаг 3
Проверяем, что в свойствах начальной сетки по Z задана одна ячейка. Все ячейки в этом направлении получаются очень сильно вытянутыми, но это не скажется отрицательно на точности расчёта. Реальная расчётная ячейка - та, что отрезана от начальной двумя плоскостями симметрии. Таким образом, начальная сетка в расчётной области получится близкой к кубической.
Шаг 4
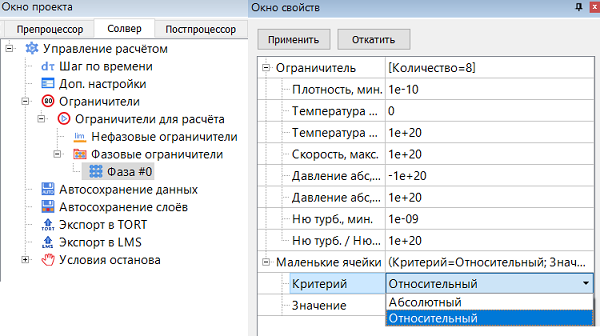
Изменим критерий малости ячеек с абсолютного на относительный.
Иначе весь объем заполнится маленькими ячейками из-за того, что реальные ячейки существенно меньше начальных.
Если этого не сделать, все маленькие ячейки сольются в одну большую расчетную ячейку и расчетная область не будет разрешена сеткой.
Шаг 5
Проверяем, что адаптация активна и запускаем расчёт. Сетка адаптируется как и раньше, во всех трёх направлениях, но в направлении Z разбиение ячеек происходит вне расчётной области. Как результат, по толщине всегда остаётся только 1 ячейка. Поэтому итоговое количество расчётных ячеек в 2 раза меньше нашего первого расчёта, а именно 288 798 ячеек.
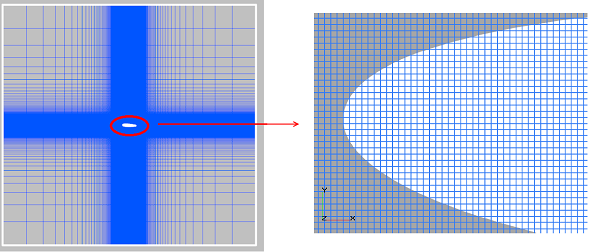
Ниже показано, как выглядит сетка по толщине. Красный прямоугольник - это поперечное сечение расчётной области, зеленая линия - край последней проадаптированной ячейки (максимальный уровень адаптации). На рисунке видно, что по толщине расчетной области везде имеется только одна ячейка, несмотря на адаптацию.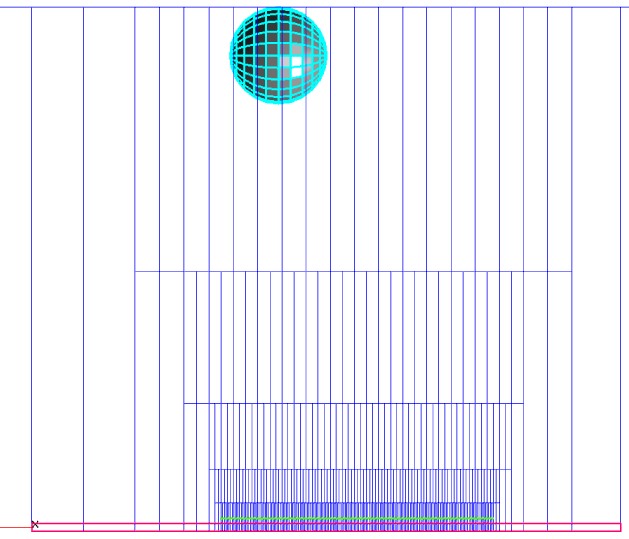 
Если в процессе расчёта появится желание увеличить уровень адаптации, необходимо отдалить нерасчётную подобласть дальше в соответствии с формулой.
post scriptum
Посмотреть результат использования удалённой нерасчётной подобласти можно в учебнике.
Кстати, этот приём изобрёл пользователь FlowVision из ИВТАНа, Александр Фирсов. За что ему огромное спасибо!
Если у вас тоже возникают идеи - не стесняйтесь поделиться ими с нами, пишите на support@flowvision.ru