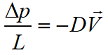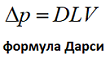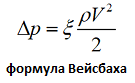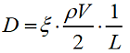В 1856 году французский гидравлик Анри Дарси экспериментально получил уравнение баланса импульса для медленного стационарного течения несжимаемой жидкости в пористой среде:
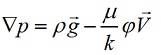
Сегодня это уравнение так и называется - «закон Дарси» - и активно применяется в гидравлике малых скоростей при моделировании течений в трубопроводах и пористых средах.
Область применения модели движения Дарси
Модель Дарси определяет линейную зависимость между градиентом давления и скоростью фильтрации. Но такое допущение возможно только для медленных течений с числом Рейнольдса Re < 2000. Однако не только скорость определяет область применения модели.
При моделировании неньютоновских жидкостей (например, нефти) связь между градиентом давления и скоростью фильтрации вероятнее всего будет описана нелинейным или дифференциальным законом. В этом случае применимость модели Дарси ставится под вопрос.
Успешный опыт применения модели Дарси продемонстрирован не только на трубопроводных задачах, но и при моделировании течения в теплообменниках, пропитки пористых композитных материалов, а также в задачах термо- гравитационной конвекции, оценки водопроницаемости грунтов и др.
Математическая основа закона Дарси
Рассмотрим более детально уравнение Дарси: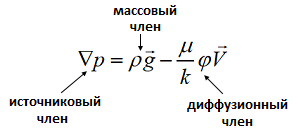 
p [Па], ρ [кг/м3], V [м/с] – давление, плотности и скорость жидкости;
μ [Па⋅c] – динамическая вязкость жидкости;
g [м/с2] – ускорение свободного падения;
k [м2] , φ [ - ] – коэффициент проницаемости и пористость среды.
Можно заметить, что по своей структуре уравнение Дарси очень похоже на другое популярное и более каноническое уравнение движения – уравнение в форме Навье - Стокса:
И это не случайность. На самом деле закон Дарси – это частный случай уравнения в форме Навье-Стокса (Н-С) для несжимаемого медленного течения.
Преобразуем уравнение в форме Навье-Стокса к уравнению Дарси
- Запишем условие несжимаемости среды, полученное из уравнения неразрывности:
При медленных течениях, влияние инерционных сил много меньше влияния вязкостных. Следовательно, ускорением (∇V) можно пренебречь, и при осреднении конвективный и нестационарный члены обратятся в ноль.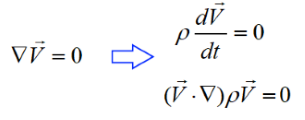
В итоге уравнение Н-С для несжимаемой жидкости принимает вид:
Уравнение Дарси — это частный случай уравнения движения в форме Навье-Стокса, полученное для медленных течений вязкой несжимаемой среды
От теории - к практике
Как говорилось ранее, модель Дарси хорошо зарекомендовала себя при моделировании течения в трубопроводах. Вычислим по формуле Дарси перепад давления в трубе (L = 2 м, d = 0.1 м) при течении воды со скоростью V = 0.001м/с.
Для такой постановки задачи (g = 0 м/с2, φ = 1) формула Дарси принимает вид: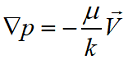 
Или, если ввести коэффициент сопротивления D [кг/с·м3]:
Вычисление коэффициента сопротивления (D)
Выведем формулу для расчёта коэффициента сопротивления D. Эта величина потребуется не только для аналитической оценки, а также и далее при создании расчётного проекта FlowVision.
Выразим коэффициент сопротивления через сопоставление уравнения Дарси с эмпирической формулой Вейсбаха для течения в круглой трубе.
Выражение для коэффициента сопротивления принимает вид:
Здесь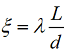 
– коэффициент гидравлических потерь (λ – коэффициент потерь на трение, L и d – длина и диаметр трубы).
Коэффициент потерь на трение вычислим по формуле Пуазейля: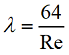
Тогда окончательная формула для коэффициента сопротивления принимает вид:
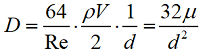Вернёмся к исходным данным задачи (μ = 0.001 Па⋅c, d = 0.1 м) и вычислим D = 3.2 кг/с·м3 .
Вычисление перепада давления (Δp)
Воспользуемся выведенным ранее уравнением движения в форме Дарси:
Подставим известные числовые значения: D = 3.2 кг/с·м3, L = 2 м, V = 0.001м/с. Отсюда потери давления между входом и выходом трубы Δp = 0.0064 [Па].
Моделирование во FlowVision
В качестве основы воспользуемся проектом обучающего примера Lam_tube. Клиентская часть проекта находится в папке с обучающими примерами в инсталляционной директории /Tutorial\Samples\RussProjects\Lam_tube.
Проведём расчёты проекта Lam_tube с использованием двух моделей движения: Навье-Стокса и Дарси.
Модель Навье-Стокса
Запустим проект на расчёт без изменений. Через 1000 секунд расчётного времени будет достигнуто стационарное значение величины давления на входе – зафиксируем его: Δp = 0.0071 [Па].
Модель Дарси
Преобразуем проект для моделирования с помощью модели Дарси.
Шаг 1. В физических процессах фазы выбираем Движение = Модель Дарси.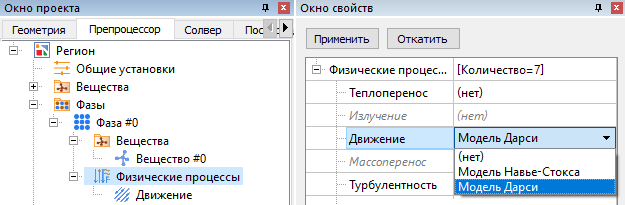
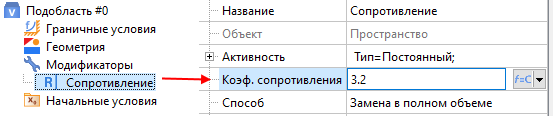
Шаг 2. Во всём расчётном пространстве задаём гидравлическое сопротивление (коэффициент D) с помощью модификатора Сопротивление.
Обязательное условие использования модели Дарси - задание дополнительного гидравлического сопротивления среды с помощью модификатора «Сопротивление» (или «Анизотропное сопротивление» — для случая пористой среды).
Если коэффициент сопротивления не задан, то для расчёта автоматически принимается, что D=1e-6. Безусловно, это обеспечивает некорректный результат перепада давления.
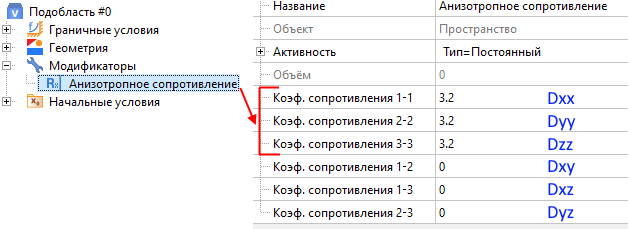
В случае использования модификатора Анизотропное сопротивление, гидравлическое сопротивление определяется симметричной матрицей проекций сопротивления по направлениям на координатные оси: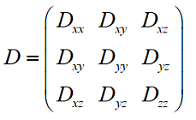
Шаг 3. Запускаем расчёт и контролируем перепад давления на графике окна мониторинга: Δp = 0.00636 [Па]. Установившееся решение достигается за 20 с расчётного времени.
Модель Дарси FlowVision согласуется с аналитикой с точностью 1%. При сравнении модели Дарси и модели Навье-Стокса разница в величине перепада давления = 10%*.
*Для уточнения расчёта по модели Дарси используйте трубу большей длины (примерно в 3 раза). В обучающем примере малая длина трубы не позволяет достигнуть установившегося ламинарного профиля скорости на выходе. Однако при увеличении длины модель Дарси максимально близко согласуется с моделью Навье-Стокса.
Основное преимущество модели Дарси заключается в быстром достижении установившегося решения: стационарное решение модель Дарси в 50 раз быстрее, чем модель Навье-Стокса.
модель Дарси для разных геометрических моделей труб
Аналитический расчёт по формуле Дарси имеет место быть только для прямолинейного участка трубы. Определение перепада давления для труб сложной формы возможно только с помощью проведения численного моделирования.
Гофрированная труба с течением воды
Сильфоны обычно применяются для компенсации температурного расширения трубопроводов, а также для предотвращения разрушения труб при их деформации.
Исходные данные задачи: L = 3 м., d = 0.1 м., V = 1 м/с.
Вычисляем коэффициент сопротивления для закона Дарси: D = 32μ / d2 = 3.2 кг/с·м3 , указываем это значение в модификаторе Сопротивление, запускаем расчёт и наблюдаем результаты.
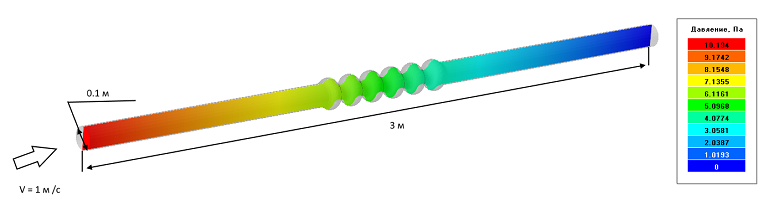Распределение давления в гофрированной трубе
Течение воды в изогнутой трубе
Изгибы труб - это обычное дело при прокладывании трубопровода в черте города. Посмотрим какой перепад давления образуется в изолированном изогнутом участке.
Исходные данные задачи: L = 7 м., d = 0.2 м., V = 3 м/с.
Вычисляем коэффициент сопротивления для закона Дарси: D = 32μ / d2 = 0.8 кг/с·м3
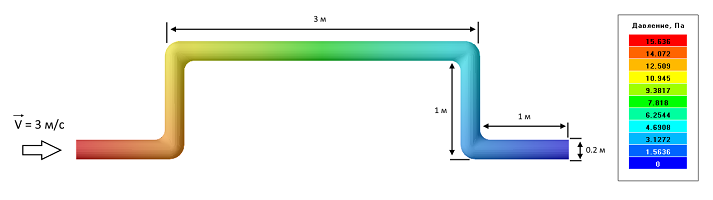Распределение давления в изогнутой трубе
Течение воды в изогнутой в трубе с изгибами в двух плоскостях
Данный пример демонстрирует более сложную пространственную конфигурацию трубопровода. Здесь уже необходимо учитывать влияние сил гравитации.
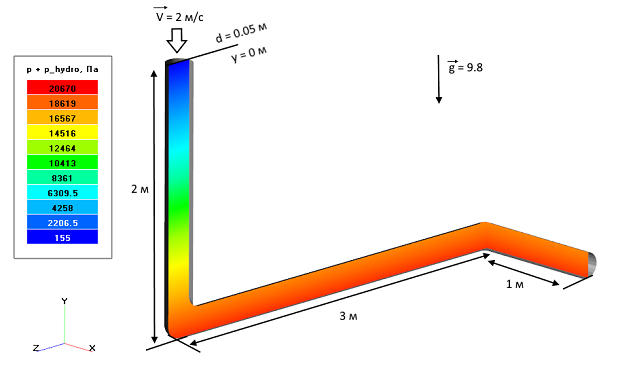
Исходные данные задачи: L = 6 м., d = 0.05 м., V = 2 м/с.
Вычисляем коэффициент сопротивления для закона Дарси: D = 32μ / d2 = 12.8 кг/с·м3
Распределение давления (с учётом гидростатики) в изогнутой трубе
Течение воды в изогнутой в трубе с фильтром
Пористая среда фильтра создаёт дополнительное гидравлическое сопротивление, которое учитывается при задании модификатора Сопротивление или Анизотропное сопротивление.
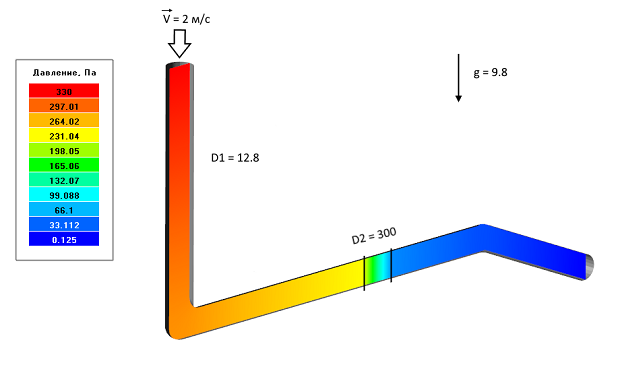
Исходные данные задачи: L = 6 м., d = 0.05 м., V = 2 м/с.
Вычисляем коэффициент сопротивления для закона Дарси: D1 = 32μ / d2 = 12.8 кг/с·м3
Коэффициент сопротивления фильтра примем D2 = 300 кг/с·м3
Распределение давления в изогнутой трубе с фильтром