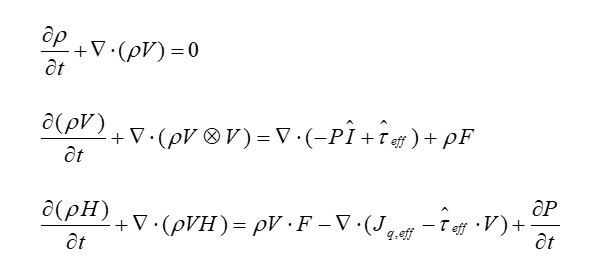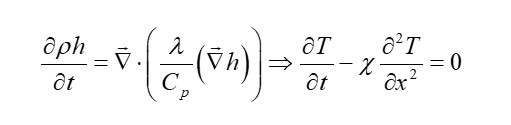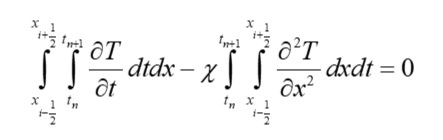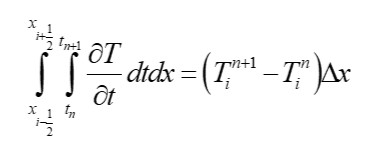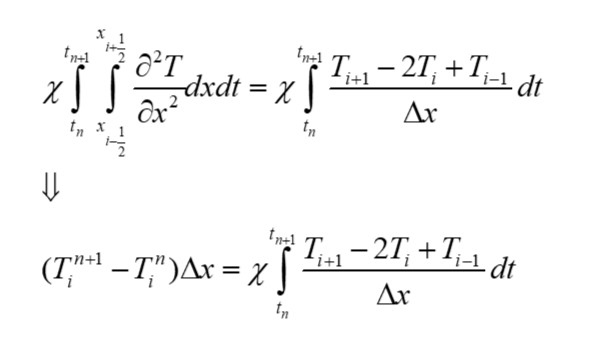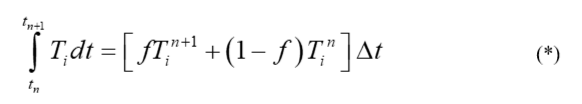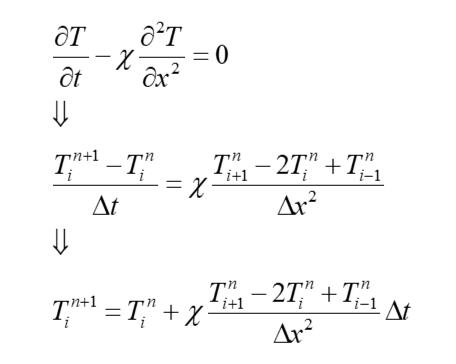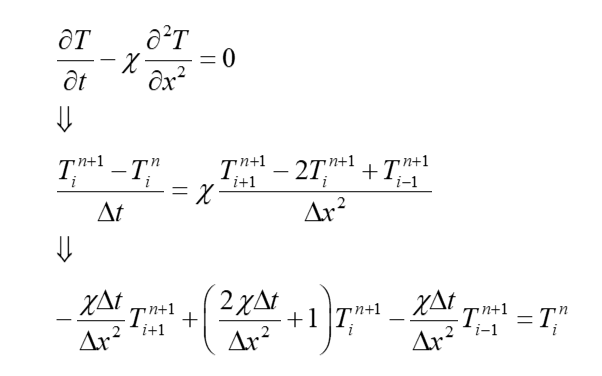Несмотря на то, что каждый пользователь CFD хотел бы по нажатию одной кнопки получить готовое и верное решение, в некоторых случаях инженеру-расчетчику может понадобиться изменить настройки численного метода в программном комплексе под свою задачу. Такая возможность есть и в FlowVision, но для этого нужно иметь некоторые представления о том, что за этими настройками стоит. В данной статье мы коснемся схем дискретизации по времени.
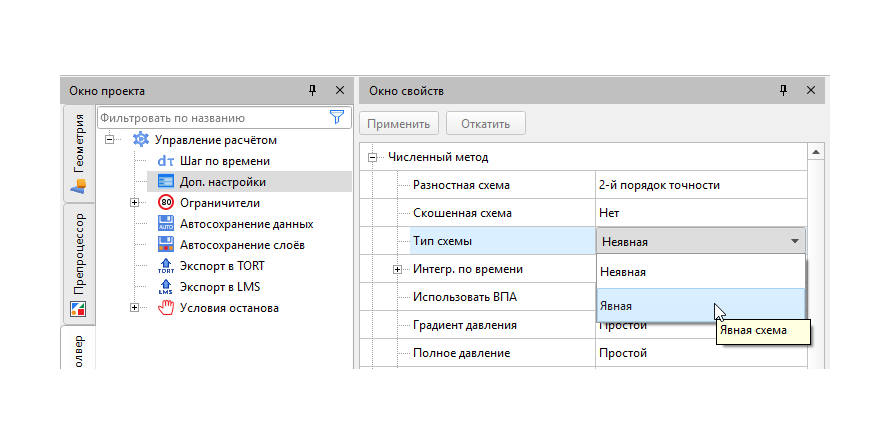
У пользователя FlowVision есть выбор между неявной и явной схемой, при этом по умолчанию всегда выбрана первая. Данная схема является абсолютно устойчивой, то есть она позволяет считать задачи с большим шагом по времени. В отличие от явной схемы, у которой есть ограничение по величине временного шага.
В то же время неявная схема обладает такими особенностями, как большее время счета и «размазывание» решения. Поэтому в ряде случаев использование явной схемы позволяет получить более быстрое или более точное решение.
Имеет смысл переключить тип схемы на явную в случаях, если моделируемый физический процесс разрешается с временным шагом равным или меньше явного. Таким образом вы сократите затрачиваемое время на итерацию и можете повысить точность решения.
Однозначно сказать, какая схема будет лучше, нельзя. Обычно неявная схема с большим шагом по времени используется в стационарных задачах. Но порой явная схема может привести к более быстрой сходимости. Бывает, что слишком большой шаг по времени в неявной схеме приводит к замедлению сходимости и выход на стационарный режим будет происходить дольше, чем если использовать эту же схему с меньшим шагом по времени.
Поэтому в любом случае мы рекомендуем проводить исследование сходимости по временному шагу при поиске стационарного решения. Попробуйте уменьшить шаг по времени и убедитесь, что решение сошлось.
В данной статье ниже мы подробнее рассмотрим оба типа расчетных схем. Вспомним, как в общем виде выглядит полная система решаемых уравнений гидро- и газодинамики:
Такая система уравнений в общем случае не может быть решена аналитически, поэтому на помощь приходят численные методы. Перечислим основные этапы численного решения:
- Дискретизация уравнений модели и граничных условий;
- Приведение дискретных аналогов в систему линейных алгебраических уравнений (СЛАУ);
- Визуализация и анализ полученного решения.
Первый пункт подразумевает использование метода сеток — расчетная область представляется в виде набора узлов. Условно, если мы считаем нагрев металлического стержня, то мы разбиваем его на несколько частей, каждая из которых имеет свою температуру. Тем самым изменение температуры, которое является непрерывной функцией, заменяем на набор дискретных значений. Чем больше разбиений, тем ближе модель к реальному объекту.
В программном комплексе FlowVision используется метод конечных объемов. Идея метода состоит в интегрировании уравнений в каждом из объемов. При таком подходе обеспечивается соблюдение консервативности: поток через грань, которая соединяет два объема, учитывается в уравнениях для обоих объемов. Таким образом, решение даже на грубой сетке удовлетворяет точным интегральным балансам массы, энергии и импульса.
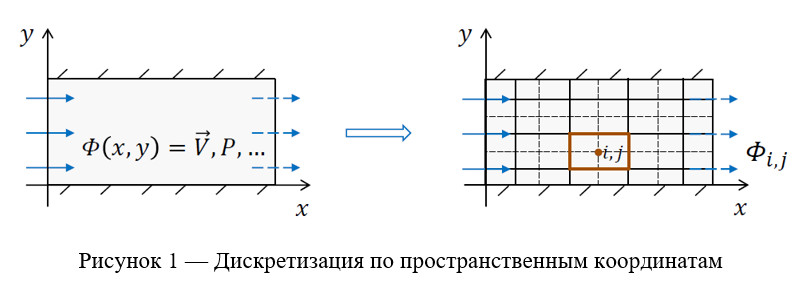
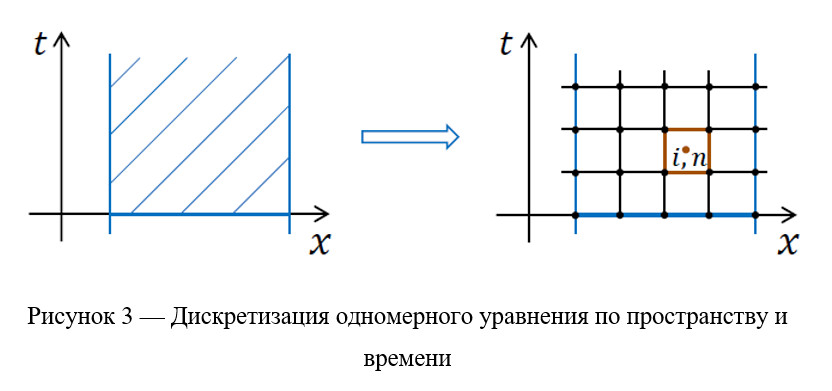
Ниже на рисунках показано разбиение сеткой расчетной области в пространственных координатах.
Здесь
— дискретное значение параметра в узле контрольного объема. Если функция
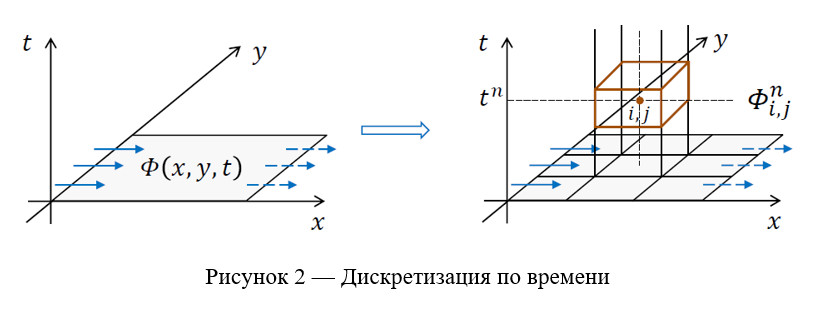
Здесь n — индекс, обозначающий соответствие дискретного значения 
временному слою tn.
Рассмотрим дискретизацию по времени на примере простого одномерного уравнения теплопереноса. Для простоты примем, что плотность, теплопроводность и теплоемкость среды постоянны, а значит:
Здесь первое слагаемое – нестационарное и показывает изменение температуры во времени. Второе слагаемое отражает диффузионный перенос физической величины. Здесь χ — коэффициент температуропроводности, который также является коэффициентом диффузии, который в нашем случае не зависит от координаты или времени.
Уравнение, приведенное выше, можно использовать для расчета теплопереноса в твердом теле. Если задача нестационарная, то нужно разбить расчетное пространство в направлении оси времени и координаты x. Тогда дискретизация данного уравнения методом конечных объемов будет выглядеть следующим образом:
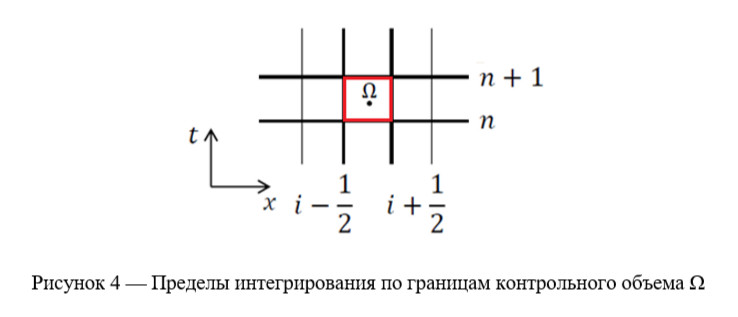
Вспоминаем, что в методе конечных объемов мы интегрируем исходные уравнения в каждом из них. Тогда уравнение теплопроводности для выделенного объема можно переписать следующим образом:
Нестационарное слагаемое можно представить в следующем дискретном виде:
А диффузионное слагаемое имеет следующий дискретный вид:
На данном этапе для вычисления интеграла по времени нужно ввести предположение относительно изменения во времени температур Ti+1, Ti, Ti-1 . Одно из таких предположений имеет вид:
Здесь ƒ — некоторый коэффициент.
Если ƒ = 0, то интеграл в левой части выражения полностью определяется температурой с шага n, то есть с предыдущего шага по времени. То есть «старое» значение 
существует в пределах всего временного шага, за исключением точки tn+1. Такой подход называется явной схемой (кривая 1 на рисунке):
В этом случае значение температуры в каждом контрольном объеме на новом шаге по времени будет определяться исходя из значений в том же и соседнем конечных объемах на предыдущем временном шаге. То есть 
не зависит от 
и 
:
Явная схема является только условно устойчивой, поэтому есть ограничение на шаг по времени задачи. Соответственно в FlowVision при выборе явной схемы нужно использовать CFL = 1 или меньше.
Неявная схема
Если же коэффициент в формуле (*) положить равным f = 1, то такой подход к разложению по времени называется неявной схемой (кривая 2 на рисунке 5). То есть в момент времени tn
Видно, что
Стоит отметить ряд особенностей, которые имеет неявная схема:
- она «медленнее», чем явная, так как нужно решать систему уравнений, а не совершать простые арифметические вычисления;
- схема безусловно устойчивая, то есть формально нет каких-то ограничений на шаг по времени, однако не стоит забывать, что расчетный шаг задачи должен охватывать характерное время физического процесса. Для стационарных задач таким характерным временем является пролетное время частицы.
- данная схема имеет такую особенность как «размазывание» решения. Так как используются значения с нового временного слоя, мы используем некое усреднение. Вдобавок, когда мы увеличиваем расчетный шаг по времени, то мы обмениваемся информацией с большим количеством ячеек. Это помогает сглаживать различные возмущения, которые и повышают устойчивость схемы. Но в то же время мы «размазываем» и не разрешаем возмущения, которые могут являться частью физического процесса.
Методы расщепления
Так как все уравнения, составляющие полную систему уравнений гидрогазодинамики, связаны между собой, то решать ее нужно совместно. Но это довольно сложная процедура, поэтому используется такой подход, когда одно уравнение расщепляется на несколько по физическим переменным, времени или физическим процессам. Затем эти уравнения считаются последовательно. Например, можно представить уравнение сохранения импульсов и неразрывности в виде двух уравнений: для скорости и для давления. Методы расщепления не являются предметом этой статьи, поэтому подробнее узнать об алгоритме можно в документации или в [О. М. Белоцерковский «Численное моделирование в механике сплошных сред». – М.: Наука, 1984].
Отметим, что явная схема в программном комплексе FlowVision на самом деле является полу-явной. Так как уравнения для давления и для плотности энергии излучения при выборе данной схемы будут считаться все равно неявным образом.
Если у вас возникли какие-либо вопросы по поводу содержания и материалов, пишите нам в Техническую Поддержку.