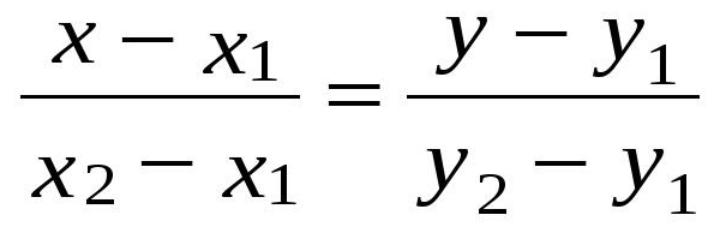Резкое изменение параметров расчета может приводить к ухудшению сходимости и даже развалу в следствие появления слишком больших градиентов физических величин.
Например, когда на определенной стадии полета по условиям задачи включаются реактивные двигатели летающего объекта: если задать сразу номинальное давление на ГУ сопел, то получится слишком большой градиент по давлению.
Другой распространенный пример: необходимо моделировать вращение ротора водяного насоса или гребного винта судна. Если расчет начать сразу с исследуемой частоты вращения, то в случае несжимаемой жидкости произойдет удар вращающегося ротора о покоющуюся жидкость с образованием бесконечных градиентов давления и, скорее всего, развал.
Резкое изменение не только физических величин может приводить к негативным последствиям: резкая адаптация на несколько уровней, резкое изменение шага по времени также можгут приводить к плохой сходимости или развалу.
Чтобы избежать негативных эффектов при изменении переменных, их можно плавно изменять с помощью уравнения в редакторе формул.
Простейший случай - изменение по линейному закону.
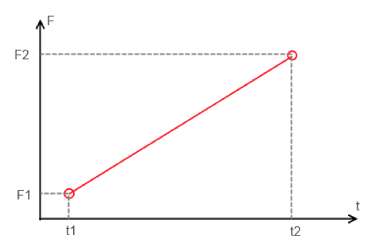
Как правило нам известно, с какой величины переменной F мы хотим начать ( F1 ) и к какой величине хотим придти ( F2 ). Также нам известно за какое время ( dt ) необходимо произвести изменение переменной и начиная с какого момента ( t1 ).
В этом случае удобно воспользоваться уравнением прямой по известным двум точкам:
Я подготовил себе удобный шаблон для редактора формул, чтобы можно было быстро задать плавное изменение величины по линейному закону:
//Здесь определяю переменную, которая будет зависеть от времени, в данном случае от номера шага
t=StepNumber;
//Здесь необходимо задать с какого значения по какое будет меняться результат этой формулы
F1=1000;
F2=11768400;
//t1 - это момент времени, с которого начнется изменение выходной переменной F
t1=625;
//Чаще всего мне удобно задать не t2, а интервал времени,
//в течение которого будет меняться переменная F.
//А t2 пусть посчитается автоматически
dt=50;
// Ниже я задаю t1 и t2.
t2=t1+dt;
//Ниже вычисляется переменная F. Если t<t1, то F=F1, если t>t2 , то F=F2,
//а между t1 и t2 происходит изменение F по линейному закону.
{
(t<t1): F1;
(t>t2): F2;
( (t>=t1) AND (t<=t2) ): (t-t1)/(t2-t1)*(F2-F1)+F1;
}
Аналогичным образом нетрудно составить выражения для квадратичного закона.