В статье рассмотрен подход к решению конвективных задача во FlowVision с применением приближения Буссинеска.
Данный подход целесообразно использовать в случае замкнутых систем (нет ГУ входа и выхода) и в случае, когда гидростатическая составляющая давления значительно больше, чем изменение давления без учета гидростатики (что характерно для задач естественной конвекции и что может приводить к потере точности решения).
Теория
При решении задач естественной конвекции нередко применяется приближение Буссинеска .
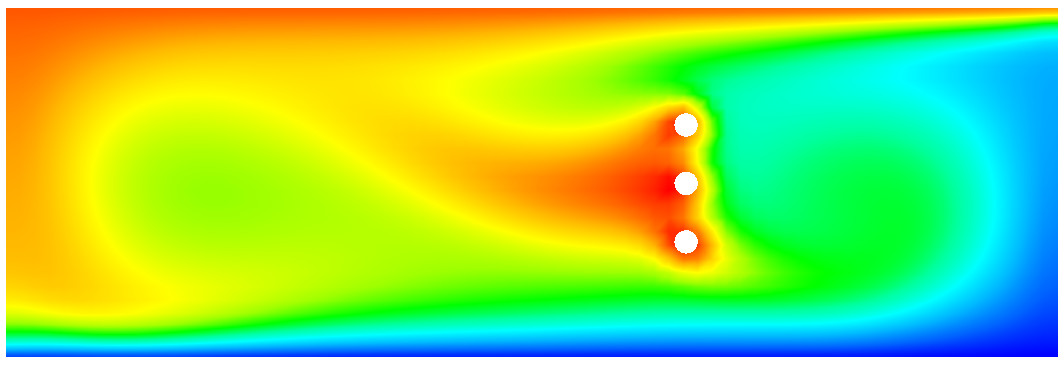
Основная идея заключается в решении системы уравнений Навье-Стокса и энергии с использованием специальной зависимости плотности от температуры только при вычислении объемной силы. Во всех остальных частях уравнений применяется константное значение плотности:
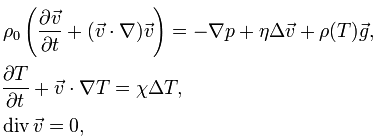
Приближение Буссинеска применимо лишь для несжимаемых жидкостей (число Маха менее 0,3).
Часто для описания зависимости плотности от температуры применяется линейная аппроксимация:
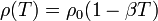
где beta — коэффициент объёмного расширения жидкости, ro _0 — плотность жидкости при некоторой равновесной температуре To, T — отклонение температуры от равновесия. Поскольку beta и отклонение температуры обычно относительно невелико, то линейное приближение обладает приемлемой точностью в большинстве исследуемых задач.
После подстановки в первое выражение представленной зависимости, также отказавшись от учета гидростатической составляющей ( от ro_0 * g ) и разделив все выражене на ro_0 получим:
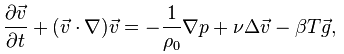
Таким образом для моделирования конвекции достаточно определить объемную силу величиной beta* (T) *g . Здесь Т = Tabs-To, где Tabs - абсолютная температура в ячейке, To - некая равновесная температура.
Во FlowVision уравнение навье стокса не делится на плотность. Поэтому формула для объемной силы будет выглядеть как beta*T*g*ro.
Если же закон описывается более сложным образом, то объемную силу во FlowVision можно определить как (ro – ro_0)*g .
Приближение Буссинеска во FlowVision
FlowVision позволяет решать задачи конвекции для сжимаемых газов прямым методом, когда во всех уравнениях учитывается переменная плотность. Однако в ряде задач целесообразно использовать приближение Буссинеска. В первую очередь в случаях, когда расчетная область замкнутая (нет входных и выходных граничных условий). Изменение плотности в замкнутой среде может приводить к существенному изменению давления в расчетной области, что негативно скажется на точности расчета. По этой же причине в задачах конвекции несжимаемой жидкости целесообразно отказаться от учета гидростатической составляющей там, где это возможно.
Итак, для решения задачи с приближением Буссинеска во FlowVision необходимы выполнить следующие настройки:
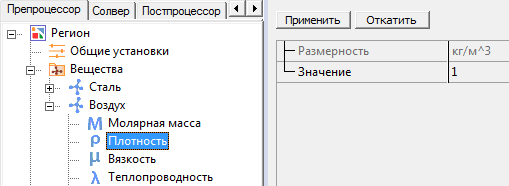
- Задать константное значение плотности
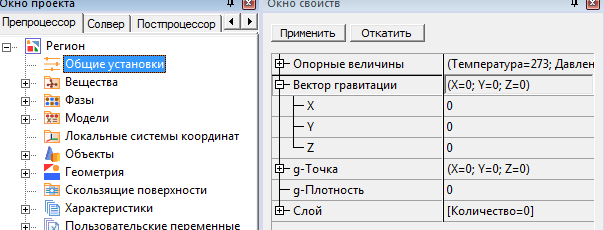
- Задать нулевой вектор гравитации
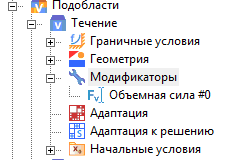
- Создать модификатор Объемная сила
- Определить с помощью редактора формул вектор объемной силы
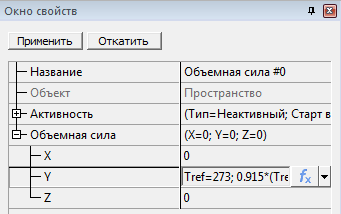
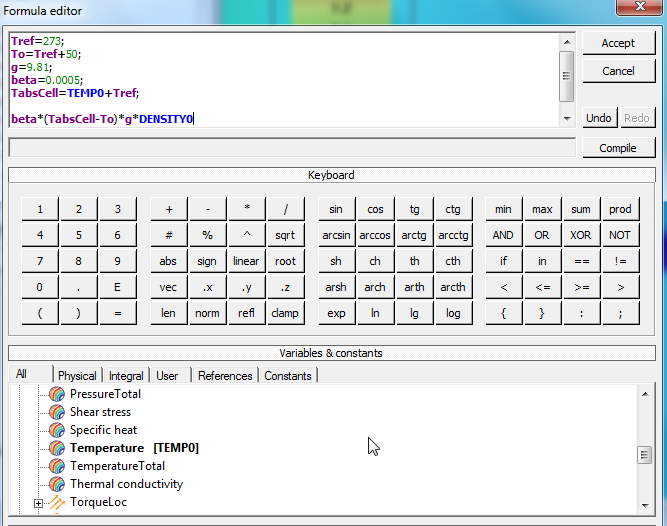
Вектор объемной силы должен рассчитываться для каждой ячейки, поэтому при определении вектора необходимо использовать локальные переменные для рассматриваемой фазы. На картинке Выше применяется локальная температура воздушной фазы. В качестве «нулевых» значений плотности и температуры при определении объемной силы целесообразно использовать начальное значение плотности и температуры, которые в идеале должны быть максимально близки к средним величинам в стационарном решении.
Не забудьте проконтролировать направление вектора объемной силы, соотнесите выбранное направление g и навпраление осей глобальной системы координат во FlowVision.
В примере выше для наглядности производится вычисление абсолютных значений температур. Если начальная температура равна нулю (абсолютная соответствует опорной), то операция эта избыточна, т.к. Tref в получившемся выражении можно сократить. Тогда выражение для объемной силы примет вид beta*(TEMP0-50) . Где TEMP0 - это фактически изменение температуры относительно 50 градусов цельсия (если опорная равна 273).
Ключевые слова: модификатор Объемная сила, приближение Буссинеска, естественная конвекция, конвекция, несжимаемая жидкость
Подготовлено с использованием возможностей следующей версии FlowVision: 3.09.04