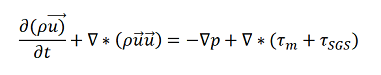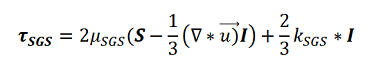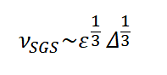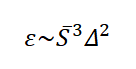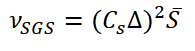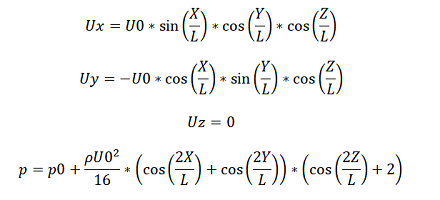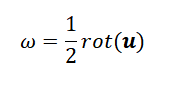Верификация LES - метода крупных вихрей

В окружающем нас мире турбулентное течение встречается гораздо чаще, чем ламинарное. Но в силу своей нестационарной природы, математическое описание турбулентности при моделировании - сложнейшая задача, интерес к которой не угасает до сих пор. В ранних статьях мы уже затрагивали тему турбулентности: описывали физику этого явления, давали определения основным параметрам и выделили три основных способа моделирования турбулентности - RANS, LES и DNS.

В этой статье мы подробнее остановимся на методе крупных вихрей, он же Large Eddy Simulation (или сокращенно, LES). 

Что такое турбулентность и как ее моделируют

Благодаря опытам Осборна Рейнольдса в конце 19 века было установлено, что существует два типа течений – ламинарный и турбулентный. В своих работах Рейнольдс впервые вывел количественную оценку перехода от ламинарного течения к турбулентному, и сегодня эта оценка носит его имя – число Рейнольдса. С тех пор гидродинамика заметно шагнула вперед, настолько, что эксперименты сегодня активно заменяются численным моделированием. Эта замена – неоспоримый прорыв научного общества, развитие цивилизации в целом. Однако вместе с теми моделями и теориями, которые появляются в огромном количестве каждый год и помогают получать более точные результаты, появляется и множество проблем, связанных с моделированием турбулентных течений.

Существует великое множество вариантов для определения термина турбулентность, что еще раз указывает на то, что описать турбулентность – трудная задача. Мы приведем термин, введенный Брэдшоу (1971 г.):

“Турбулентность – это трехмерное нестационарное движение, в котором вследствие растяжения вихрей создается непрерывное распределение пульсаций скорости в интервале длин волн от минимальных, определяемых вязкими силами, до максимальных, определяемых граничными условиями течения.”

Еще больше существует моделей, которые пытаются описать эту самую турбулентность. Каждый год появляются новые и “умирают” не прошедшие верификацию теории. Приведем здесь известную цитату Д. Лайтхилла о науке, изучающей турбулентность:

«… это кладбище теорий, на котором каждая новая теория добавляет еще одну могилу».

Однако, надеемся, читатель не подумал, что в турбулентности все так пессимистично и безнадежно. Помимо неудачных моделей существуют и такие, использование которых дает приемлемый по точности результат, и которые широко используются во всем мире.

 Существует три основных подхода к моделированию турбулентности. От простого к сложному:

• RANS (Reynolds Averaged Navier-Stokes) – наиболее распространённый в силу своей нетребовательности подход, при использовании которого рассчитываются только осредненные поля переменных. Существуют как простые алгебраические модели (типа пути смешения Прандтля), так и более сложные (типа k-ɛ, SST и др.). Более подробно о RANS моделях читайте в предыдущей статье на турбулентную тематику.
• LES (Large Eddy Simulation) – в этом подходе вихревые структуры разрешаются более детально, однако и затраты у этого метода выше (требуется большее число контрольных объемов и меньший шаг по времени). В данной статье будем рассматривать именно этот подход.
• DNS (Direct Numerical Simulation) – при таком подходе моделируются все вихри, вплоть до наименьших – Колмогоровских. Этот метод отличается большей точность относительно других, однако требует колоссальных затрат вычислительных мощностей. С развитием вычислительной техники этот метод становится всё более актуальным. Но в силу ограниченности вычислительных ресурсов, мало кто может позволить себе использование DNS подхода при моделировании.
  

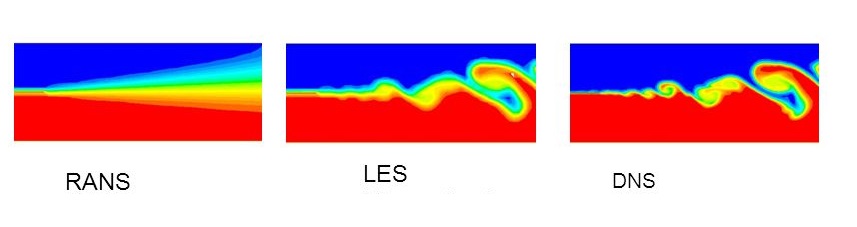
Рис 1. Результаты моделирования тремя разными методами

Перейдем к рассмотрению LES подхода.

Особенности LES подхода

В основе LES лежат уравнения Навье-Стокса, в которых напряжения разделены на сумму напряжений крупномасштабных и мелкомасштабных вихрей:

К уравнениям применяется процедура фильтрации, задачу которой обычно выполняет расчетная сетка. Выделим основную идею LES моделирования:

Точно разрешаются крупномасштабные вихри, а вклад от мелкомасштабных вихрей, которые обрезаются фильтром (сеткой), моделируются численно.

Как и в RANS подходе, для замыкания системы уравнений используется обобщённая гипотеза Буссинеска, и основной задачей является создание модели для вязкости (для RANS – турбулентной, для LES – подсеточной):

где μ_SGS – подсеточная вязкость,  S – тензор скоростей деформаций, I – единичный вектор, k_SGS – кинетическая энергия турбулентности.

Первая и наиболее распространённая модель для расчета подсеточной вязкости – модель Смагоринского.

В основе этой модели лежит предположение, что вязкость зависит от среднего значения скорости диссипации турбулентной энергии ɛ на единицу объема. Исходя из соображений размерностей следует:

где Δ – характерный масштаб фильтра (размер расчетной ячейки).

Отметим, что масштаб фильтра обычно рассчитывается как кубический корень из объема контрольного объема расчетной сетки. В связи с этим в расчетах с использованием LES подхода предпочтительна изотропная сетка, т.е. без использования сгущения сеточных линий и применения адаптаций. В таком случае масштаб фильтра постоянен для всей расчетной области и не возникает проблем с выбором его значения.

Величину ɛ можно определить также исходя из соображений размерности, при условии, что в рассматриваемом течении есть выраженный инерционный интервал. На этом интервале работает закон Колмагоровского спектра:"-5/3".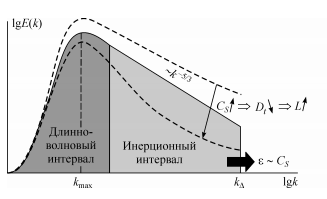 

Рис.2 Обрезанный фильтром спектр турбулентных пульсаций [1]

На рисунке представлен спектр турбулентных пульсаций, где k_Δ- предельное волновое число, после которого сигнал обрезается фильтром. На этом рисунке можно качественно понять, в чем смысл подхода LES, - разрешается основная часть спектра, имеющая низкие частоты, т.е. вихри крупного масштаба (длинно-волновой и инерционный интервал). После k_Δ начинается диссипативный интервал (высокие частоты), т.е. фактически не рассматриваются мелкомасштабные вихри, в которых происходит основная диссипация турбулентной энергии (распад Колмогоровских вихрей).

Отметим требования к течениям, моделируемым с помощью LES подхода:

1. Чем больше расчетных ячеек, тем меньше размер фильтра, тем больше k_Δ, т.е. разрешаются более высокочастотные (мелкие) вихри.

2. В спектре должен быть протяженный инерционный интервал, т.е. число Рейнольдса для рассматриваемого течения должно быть больше критического для данного типа течений.

3. Необходима достаточно малая характерная величина фильтра, которая обеспечит разрешение основного участка инерционного интервала.

Если эти требования выполняются, то исходя из соображений размерности выразим скорость диссипации:

где  – средняя скорость деформации, а 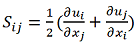  – элемент тензора скоростей деформации.

 

Следовательно, вязкость можно выразить следующим образом:

где С_s – константа Смагоринского.

Константа Смагоринского

Эмпирическая константа, которая имеет разные численные значения, как для разных типов течений, так и для разных ячеек в пределах одного течения. В качестве упрощения широко используется “статическая” модель Смагоринского, в которой константа принимается постоянной во всем объеме течения. Однако существуют и более сложные “динамические” модели Смагоринского, в которых значение константы является функцией от времени и пространства. Мы будем рассматривать стандартную модель – статическую.

В самом общем случае при выборе значения константы Смагоринского можно руководствоваться следующим:

• С_s = 0.2 - для свободных течений;
• С_s = 0.1 - для течений, ограниченных стенкой.

Однако если требуется более высокая точность получаемых результатов, константу нужно подбирать исходя из результатов верификации расчетного кода на типичных задачах.

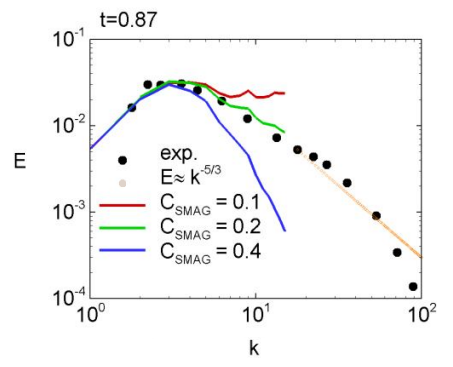Рис. 3 Сравнение спектра, полученного при использовании разных значений константы Смагоринского с экспериментальными данными и законом "-5/3" [2]

Особенностью верификации константы Смагоринского является то, что эта константа сильно зависит от используемого численного метода. Из-за этого калибровка константы должна производиться для каждого метода путем подбора значения, при котором результат лучшим образом коррелирует с условно точным решением (экспериментом или данными, полученными при использовании DNS). Зависимость значения константы от метода связана с тем, что каждый численный метод обладает численной диссипацией, т.е. сам метод в какой-то мере является фильтром и обрезает часть пульсаций. Если диссипация метода велика, то константу нужно уменьшить. И, наоборот, в методах с незначительной численной диссипацией константу нужно увеличить. В связи с этим противопоточные схемы, которые широко используются для RANS подхода, оказываются непредпочтительными для моделирования с использованием LES в силу своей чересчур большой численной диссипации. Более предпочтительными являются схемы высоких порядков аппроксимаций (от 2 и выше).

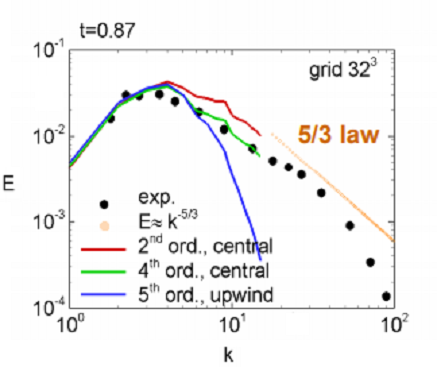Рис.4 Сравнение спектра, полученого при использовании центрально-разностных схем 2-го и 4-го порядка аппроксимации, противопоточной схемы 5-го порядка с экспериментальными данными и законом "-5/3" [2]

Повышение порядка аппроксимации центрально-разностной схемы улучшает результаты моделирования, но противопоточная схема даже 5-го (!) порядка аппроксимации дает неудовлетворительный результат. Во FlowVsion реализован численный метод 2-го порядка аппроксимации, так как схемы 4-го порядка используются крайне редко и высоких затрат вычислительных ресурсов. При этом схема 2-го порядка подходит практически для всех типов расчетов и дает удовлетворительные результаты (смотри результаты ниже).

LES во FlowVision

В данном разделе опишем, как использовать LES подход для моделирования турбулентных течений во FlowVision.

Для Фазы, в которой предполагается турбулентное течение, во вкладке Препроцессор>Регион>Фазы>Фаза#0>Физические процессы задайте:

Турбулентность = Sm

Данный параметр означает, что задана модель Смагоринского.

Для задания константы Смагоринского перейдите во вкладку Препроцессор>Регион>Фазы>Фаза#0>Физические процессы>Турбулентность и задайте:

Cs = от 0.1 до 0.24

 Рекомендации для проектов FlowVision при моделировании с LES

• Задайте в начальных условиях параметры турбулентных потоков, формирующие вихри: пульсации и масштаб турбулентности;
• Задайте нестационарные входные граничные условия (подробнее об этом приёме мы уже писали в этой статье). Часто нестационарность задаётся как профиль скорости, на который накладываются случайные синусоидальные возмущения;
• Задавайте сетку без сгущения сеточных линий и без применения адаптаций;
• Проводите исследование сходимости по сетке и по шагу по времени;
• Используйте максимально возможный порядок аппроксимации – 2-ой. 

Задача о вырождении изотропной турбулентности

Как было сказано выше, подбор константы Смагоринского должен производиться для каждого численного метода индивидуально. Для свободных течений классической верификационной задачей является задача о вырождении изотропной турбулентности на примере затухании вихрей Тейлора-Грина. Проведем проверку константы, которая задана во FlowVision по умолчанию, на примере этой задачи (по умолчанию C_S=0.17).

Расчетной областью является куб со стороной 2πL (в нашем случае πL  = 0.016), в качестве вещества используется азот, начальная плотность которого определяется уравнением идеального газа. Начальное число Маха примем равным 0.1, из него рассчитаем характерную скорость - U0. В начальных условиях зададим значения для скорости и давления, которые отвечают вихрям Тейлора-Грина:

, где U0=Ma*c_so – характерная скорость, Ma=0.1 – начальное число Маха, c_so=337 м/с – скорость звука в азоте, p0=ρ₀RT₀ - давление,  R=297 Дж/кг*К – газовая постоянная азота, T₀=297 К – начальная температура.

На всех сторонах куба заданы периодические граничные условия, что отвечает свободному течению без стенок.

Для наглядной визуализации будем использовать объемную визуализацию проекции на ось Z в интервале от -0.7 до 0.7:

Отметим, что для удобства сравнения результатов из различных источников часто используются безразмерные величины. В данной статье все величины приведены в безразмерном виде. Все расчеты мы проводили, естественно, во FlowVision, а результаты сравнивали с результатами моделирования методом DNS [3].

Перейдем к результатам

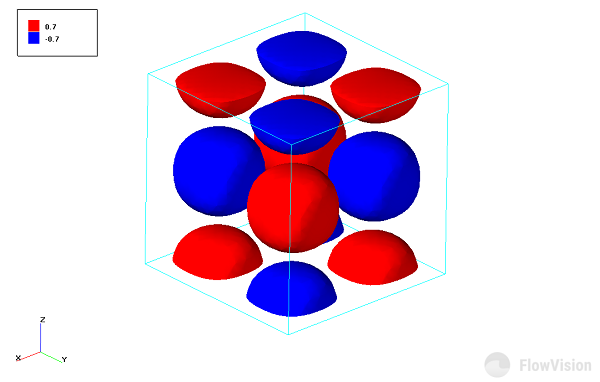
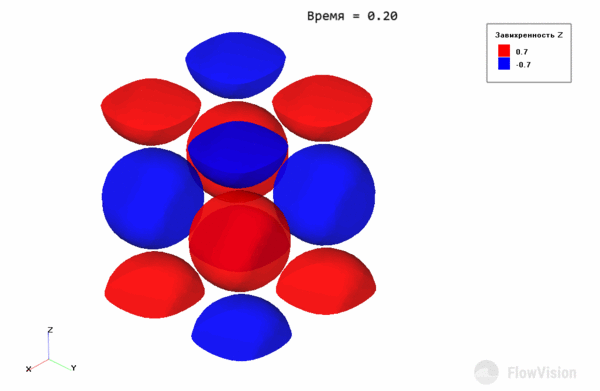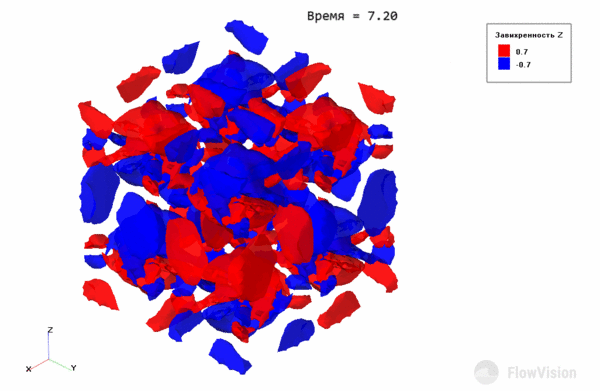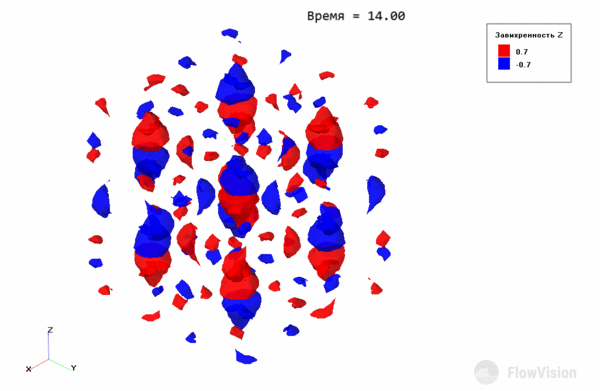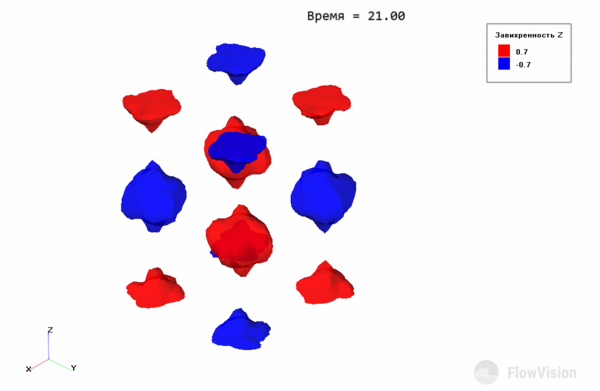
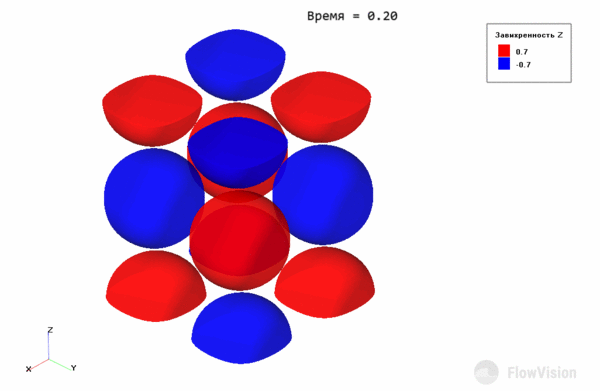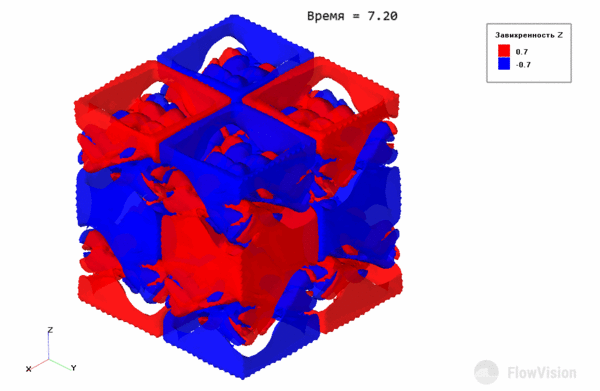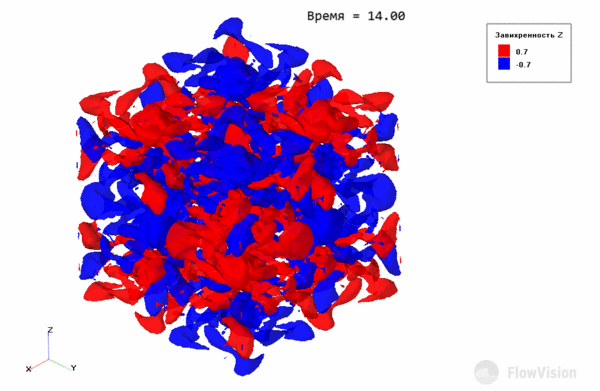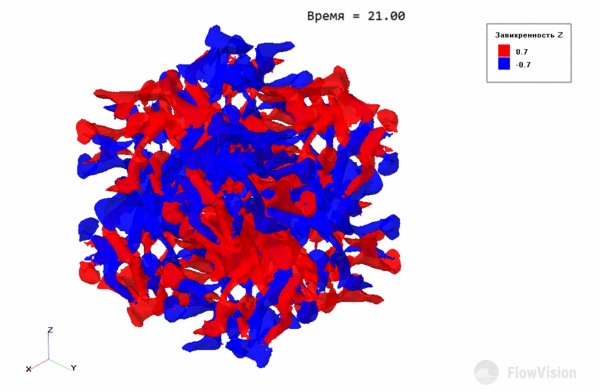
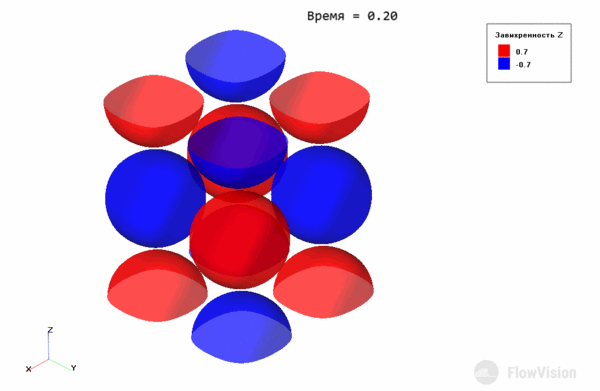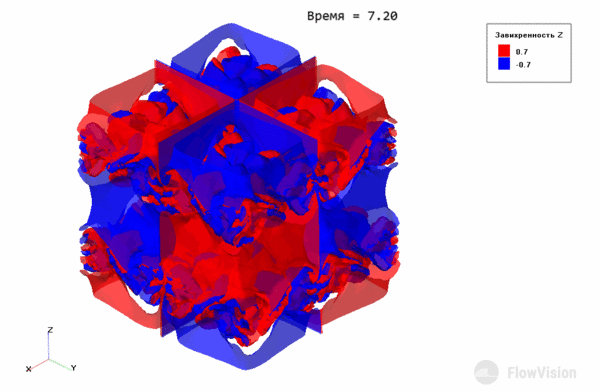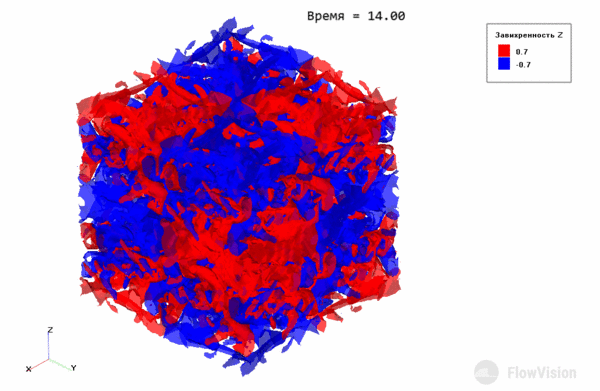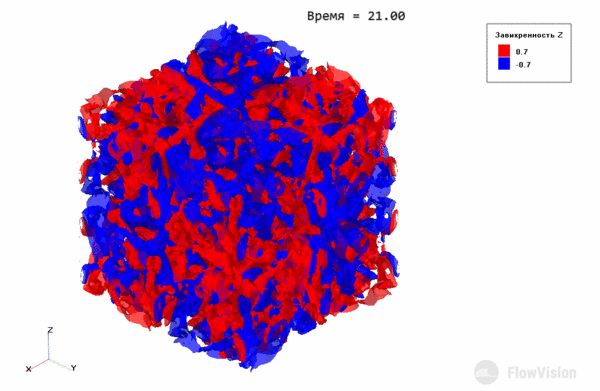
В начальный момент времени имеем вихри:

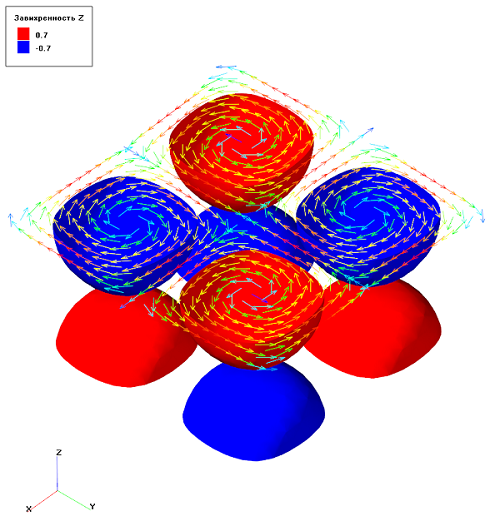
Рис.5 Поле проекции на ось Z завихренности в начальный момент времени

На рисунке 4 каждый “шар” отвечает отдельному вихрю.  Там, где проекция завихренности отрицательна (синие зоны), вихри закручены по часовой стрелке относительно оси Z, где положительна (красные зоны) – против.

Рис. 6 Вектора скорости показывают направление вращения вихрей

Эволюция вихрей Тейлора-Грина выражается в постепенном распаде крупных вихрей на более мелкие за счет диссипативных процессов. С течением времени вихри становятся такими маленькими, что отчетливой структуры течения не наблюдается.

Gif-анимация распада на сетке 32³

В ходе моделирования использовались сетки с одинаковым количеством ячеек по каждой из осей, равным 32, 64, 128, 256.

В качестве контрольных параметров используем кинетическую энергию турбулентных пульсаций Ek и скорость диссипации кинетической энергии ɛ:

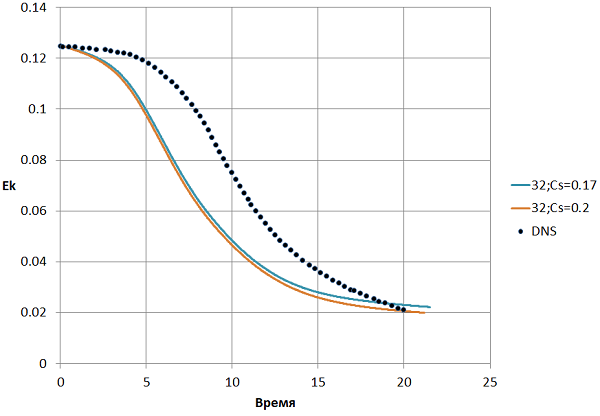
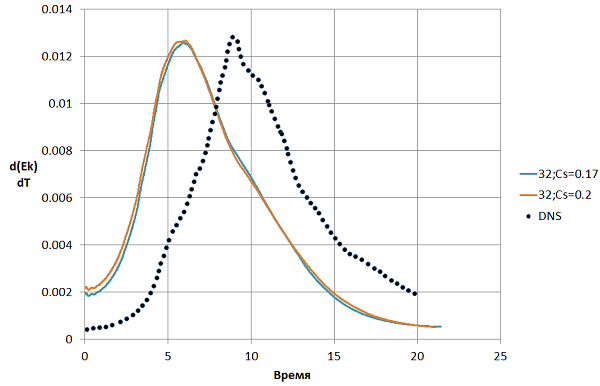
Для начала проведем показательный расчет на сетке 32³ и определимся с величиной константы Смагоринского.

Рис. 7 Зависимость турбулентной энергии от времени для разных C_S

Рис.8 Зависимость скорости диссипации турбулентной энергии от времени для разных C_S

Как видно, значение 0.17, установленное во FlowVision по умолчанию, дает более близкое к DNS результату решение. Дальнейшие расчеты будем проводить при Сs=0.17.

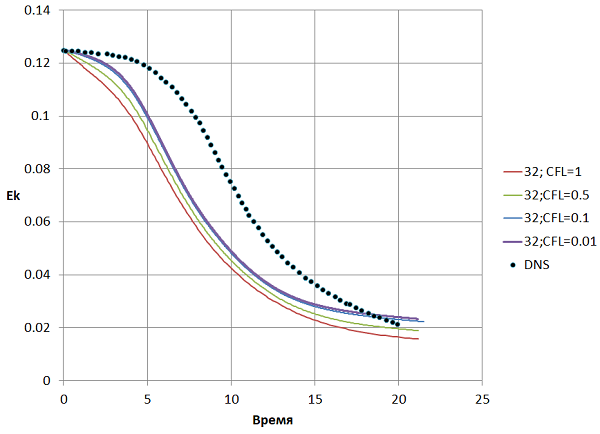
Затем выберем оптимальный шаг по времени, ориентируясь на число CFL (число Куранта-Фридрихса-Леви).

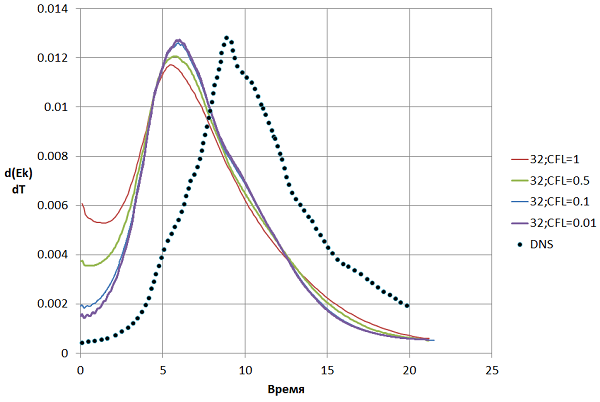
Рис. 9 Зависимость турбулентной энергии от времени для разных чисел CFL

 

Рис.10 Зависимость скорости диссипации турбулентной энергии от времени для разных чисел CFL

Различие результатов при использовании шага по времени по CFL=0.1 и CFL=0.01 незначительно, однако второй вариант требует в 10 раз больше расчетного времени. Далее все результаты будут приведены для CFL=0.1.

Рассмотрим результаты, полученные на различных сетках.

Gif-анимация распада на сетке 64³ 

Gif-анимация распада на сетке 128³

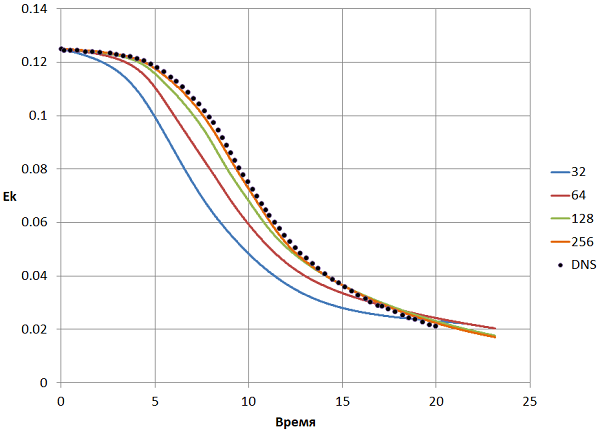
Рис. 11 Зависимость турбулентной энергии от времени для разных сеток

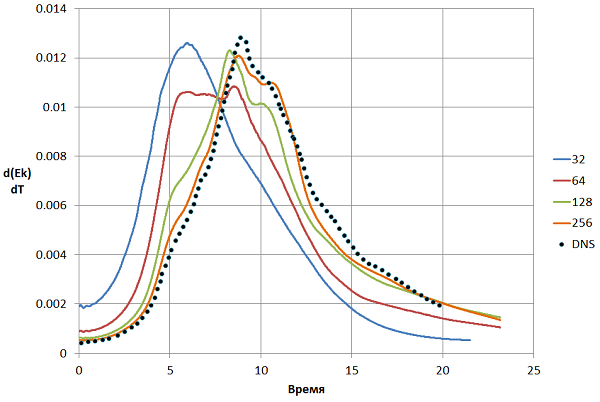
Рис.12 Зависимость скорости диссипации турбулентной энергии от времени для разных сеток

Видно отчетливое улучшение точности результатов при измельчении сетки, и при 256³ ячейках результат почти точно ложится на результаты DNS. Стоит учитывать, что за точность, которую обеспечивает LES подход, приходится платить количеством ячеек, равным 256³=16.7 млн, а расчет занимает относительно много времени, даже при использовании вычислительных ресурсов мощных кластеров.

Заключение

В качестве выводов выделим следующие тезисы:

• на примере известной задачи о вырождении изотропной турбулентности было проведено исследование сходимости по сетке и шагу по времени. Оптимальная для проведения расчётов сетка содержит 256³ ячеек, оптимальный шаг по времени - CFL=0,1;
  
  
• константа Смагоринского, установленная во FlowVision по умолчанию, обеспечивает приемлемую точность при расчёте свободных течений;
  
  
• для реализации LES подхода требуются значительные вычислительные ресурсы;
  
  
• Метод LES требует калибровки константы Смагоринского для разных типов течений и для разных расчетных комплексов.
  
  

Повторим вышеописанные рекомендации для проектов с LES

• Задайте в начальных условиях параметры турбулентных потоков, формирующие вихри: пульсации и масштаб турбулентности;
• Задайте нестационарные входные граничные условия. Часто нестационарность задаётся как профиль скорости, на который накладываются случайные синусоидальные возмущения;
• Задавайте сетку без сгущения сеточных линий и без применения адаптаций;
• Проводите исследование сходимости по сетке и по шагу по времени;
• Используйте максимально возможный порядок аппроксимации – 2-ой. 

Теперь у читателей нашего блога, незнакомых с методом LES, сложилось некоторое представление о нем. Если у Вас остались какие-то вопросы, замечания, или предложения – пишите нам в тех.поддержку, мы оперативно ответим и проконсультируем.

Заметим, что мы провели верификацию для свободных турбулентных течений без стенок. Если нужно моделировать, к примеру, течение воды в трубе, константу Смагоринского необходимо будет уменьшить.

Список литературы

1. Илюшин Б. Б., Красинский Д. В. Моделирование динамики турбулентной круглой струи методом крупных вихрей //Теплофизика и аэромеханика. – 2006. – Т. 13. – №. 1. – С. 49-61.
2. Гарбарук А. В., Стрелец М. Х., Шур М. Л. Моделирование турбулентности в расчетах сложных течений. – 2012.
3. http://www.as.dlr.de (German Aerospace Center)