Турбулентное течение – это поток, движение которого беспорядочно во времени и пространстве. Численное моделирование турбулентных течений требует нестандартного подхода к реализации. Используя подходы к моделированию турбулентных течений, описанные в этой статье, можно разобраться в основных принципах учёта турбулентности при расчёте, и даже добиться схожести с физическим экспериментом.
Рассмотрим задачу получения дорожки Кармана при обтекании куба турбулентным водным потоком со скоростью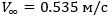 
.
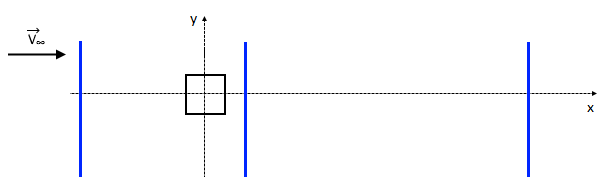
Постановка данной задачи - повторение эксперимента, описанного в статье. Оценкой правильности расчёта являлось совпадение с полученным экспериментально профилем скорости в разноудалённых от куба сечениях.
Рис. 1. Контрольные сечения
Основные моменты, о которых следует знать, задавшись целью расчёта турбулентного течения:
- Выбор модели турбулентности
- Задание начального возмущающего воздействия
- Влияние входной турбулентности
- Вариация параметров модели турбулентности
- Использование пристеночных функций
Теперь расскажем подробнее.
Выбор модели турбулентности
Для учёта турбулентности при расчёте во FlowVision используют осреднённые по числу Рейнольдса уравнения движения Навье-Стокса. Однако в результате такого осреднения появляется дополнительный неизвестный параметр – турбулентная вязкость ( µтурб [Па·с] ). Для замыкания системы уравнений применяют различные модели турбулентности, описывающие распределение поля турбулентной вязкости.
Во FlowVision реализована возможность использования семи моделей турбулентности. Причём ключевым аргументом при выборе одной из них является поиск приемлемого компромисса между физической адекватностью модели и уровнем её вычислительной трудоёмкости.
В таблице приведены средние отклонения расчётных данных от экспериментальных для задачи турбулентного обтекания куба, применимые к использованию наиболее известных двухпараметрических моделей турбулентности:
- объединённой ( k - ω + k - ε ) модели - SST
- k - ε модели - KES
- модифицированной k - ε модели – KEFV
| Модель турбулентности | Δср, % |
| SST | 6 |
| KEFV | 10 |
| KES | 17 |
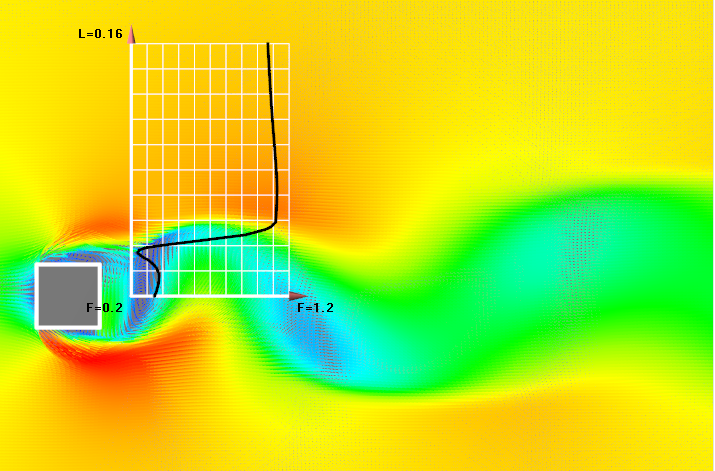
Модель SST наиболее близка к эксперименту.
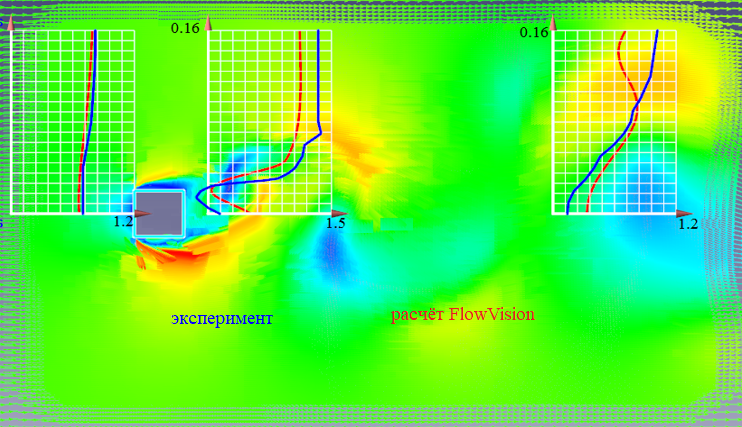Рис. 2. Сравнение профиля скорости (экспериментального с расcчитанным) для SST модели в один момент времени для выбранных контрольных сечений
Выбирая модель турбулентности, опирайтесь на статистику применения этой модели и рекомендации, которые можно найти в нашем блоге и документации FlowVision. При возникновении сомнений, проведите своё исследование, варьируя основные модели турбулентности и сравнивая их по физической применимости и быстродействию.
Задание начального возмущающего воздействия
При использовании в расчёте симметричной геометрии, образование вихрей может происходить очень медленно из-за численных эффектов. Поэтому расчётное время до момента начала вихреобразования и выхода на стационарный режим очень велико. Но если внести возмущения в поток в начальный момент времени, то сходимость наступает быстрее.
Теперь давайте «возмутим» поток. Основная идея – кратковременно изменить направление потока и таким образом добиться нестационарности в области возмущения.
Задать возмущение можно несколькими способами:
- Изменяя положение подвижного тела (на первых 2-3 шагах меняется положение тела в плоскости поперёк потока);
- Задавая отклонение векторов скорости (начальные условия вокруг тела, отклонение вектора скорости на несколько градусов от скорости набегающего потока).
Как видно на рис.3 - результаты говорят сами за себя. Для KEFV - модели время выхода расчёта «на режим» уменьшилось более чем в 5 раз: развитую вихревую структуру можно наблюдать уже на 5 секунде, в то время как, без «искусственного» возмущения, поток ещё долго остаётся симметричным.
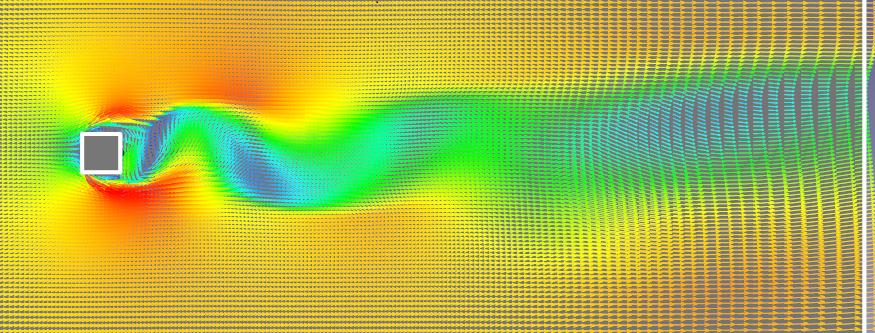Рис.3. Сравнение картин течения для KEFV- модели в момент времени t=5 сек без возмущения (сверху) и с ним (снизу).
Чтобы учитывать турбулентность с первых итераций расчёта, искусственно возмутите поток.
влияние входной турбулентности
Часто в описании физического эксперимента присутствует значение уровня турбулентности потока. В решаемой задаче об обтекании куба он равен 2%. Во FlowVision уровень турбулентности задаётся с помощью пульсаций.
Необходимо понимать, что при проведении эксперимента величина турбулентности, которая будет оказывать влияние на поток непосредственно перед обтекаемым телом, зависит от расстояния между турбулизирующим устройством и объектом.
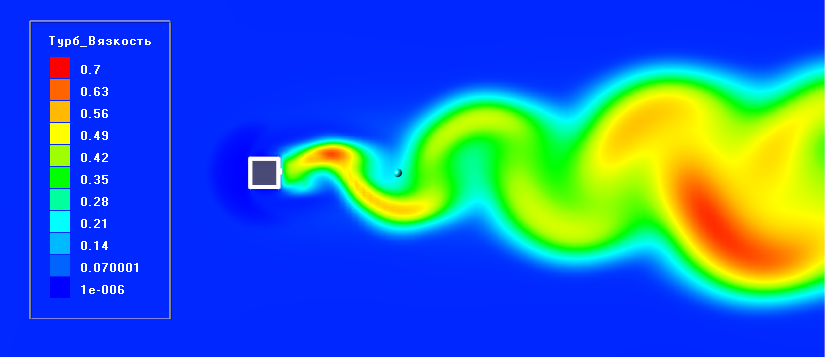
Входная турбулентность в первую очередь влияет на величину турбулентной вязкости. При задании нулевых параметров входной турбулентности, максимальное значение турбулентной вязкости уменьшилось практически на 40%. В свою очередь это обеспечивает образование в потоке вихрей с меньшей кинетической энергией.
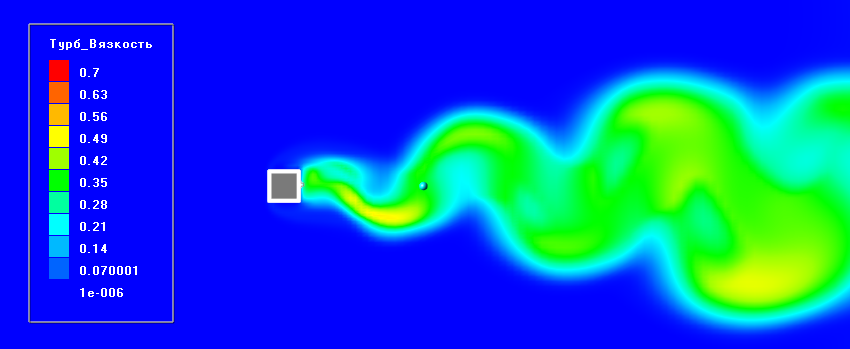
Рис. 4. Распределение поля турбулентной вязкости при задании турбулентности 2% (сверху) и 0% (снизу)
При возможности, задавайте начальные условия потока максимально приближенно к эксперименту.
Вариации параметров модели турбулентности
Во FlowVision есть возможность при задании модели турбулентности SST использовать для расчёта один из трёх способов определения кинетической энергии турбулентности и один из двух – удельной энергии диссипации энергии . Варьируя их, можно задать во FlowVision модель SST шестью разными способами.
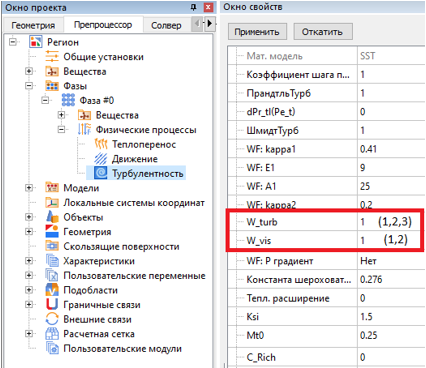Рис. 5. Способ изменения профиля k и ω во FlowVision
В таблице представлены результаты расчёта (продольной Fx и нормальной Fy сил) фиксированного отрезка времени (10 секунд) в случаях разного задания SST модели. При расчётах получаются различные результаты. Но максимальное отклонение между ними невелико – всего 5%.
| Wturb / Wvis | t, c | |Fx ср|·10-2, H | Fy ср·10-2, H |
| 1 / 1 | 10 | 1.166 | 1.091 |
| 1 / 2 | 1.165 | 1.092 | |
| 2 / 1 | 1.161 | 1.098 | |
| 2 / 2 | 1.159 | 1.101 | |
| 3 / 1 | 1.164 | 1.095 | |
| 3 / 2 | 1.164 | 1.095 |
Вариация профилей k и ω не оказала существенного влияния на результаты данного расчёта. Можно использовать стандартный способ определения этих параметров (W_turb=1, W_vis=1).
использование пристеночных функций
Применение пристеночных функций позволяет не разрешать часть турбулентного пограничного слоя, примыкающего к твёрдой поверхности. Это существенно сокращает требуемые вычислительные ресурсы.
Рекомендации по использованию пристеночных функций определяется величиной y+- безразмерным расстоянием от первого узла сетки до стенки .
Величина y+ влияет на точность расчёта сил трения, массо-, теплопередачи и другим параметров. Но не всегда требуется измельчать сетку, чтобы добиться точных результатов. Используйте пристеночные функции с учётом следующих рекомендаций:
| y+ > 1 | Пристеночные функции, равновесие |
| у+ ≤ 1 | Нет пристеночных функций |
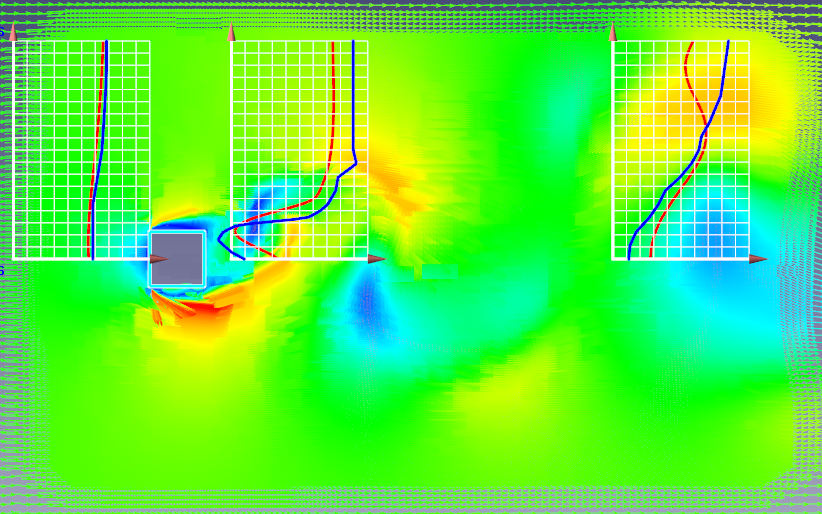
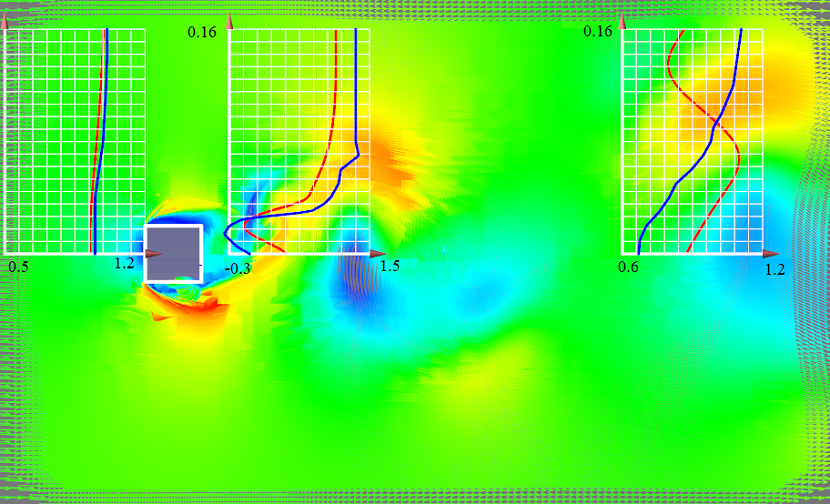
Ниже представлены картины течения в окрестности куба в случае высокорейнольдсового и низкорейнольдсового расчётов при использовании SST модели.
При расчёте с низкими значениями , профиль скорости наиболее близок к полученному в эксперименте. Рассогласование для сечения, находящимся непосредственно за кубом, составило 12% и 21% для низко- и высокорейнольдсового расчётов соответственно.
Однако для достижения столь точных результатов требуется более подробная сетка. В этом случае, при измельчении сетки, количество расчётных ячеек увеличилось на 23%.
 |
|
||||
 |
|
Рис.6. Сравнение профилей скорости (экспериментального и рассчитанного) для SST модели в один момент времени в случае включения (сверху) и выключения (снизу) пристеночных функций в зависимости от величины y+
Следует помнить, что для достижения более точных результатов требуется измельчение расчётной сетки. Необходимо проводить исследование сходимости по сетке, чтобы определить оптимальный инструмент расчёта, для которого достигается приемлемая точность при использовании меньших вычислительных мощностей.
Использование пристеночных функций для высокорейнольдсовых расчётов (y+ >1) обязательно, так как пристеночные функции обеспечивают получение физически правильного решения.