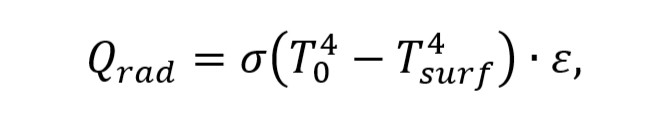В версии FlowVision 3.15.01 была реализована возможность моделирования отвода тепла с поверхности с помощью закона Стефана-Больцмана без включения моделей излучения. В статье сравниваются новый и ранее доступные методы учета отвода тепла излучением с поверхности.
В промышленности существует множество инженерных задач, в ходе которых требуется моделировать теплообмен и тепловое излучение, поскольку необходимо точно прогнозировать температурные поля, чтобы избежать перегрева оборудования, обеспечить надежность и энергоэффективность конструкций. Особенно это важно в процессах, где высокие температуры влияют на прочность материалов, устойчивость систем или безопасность, к примеру:
- Процессы теплообмена в печах и топках;
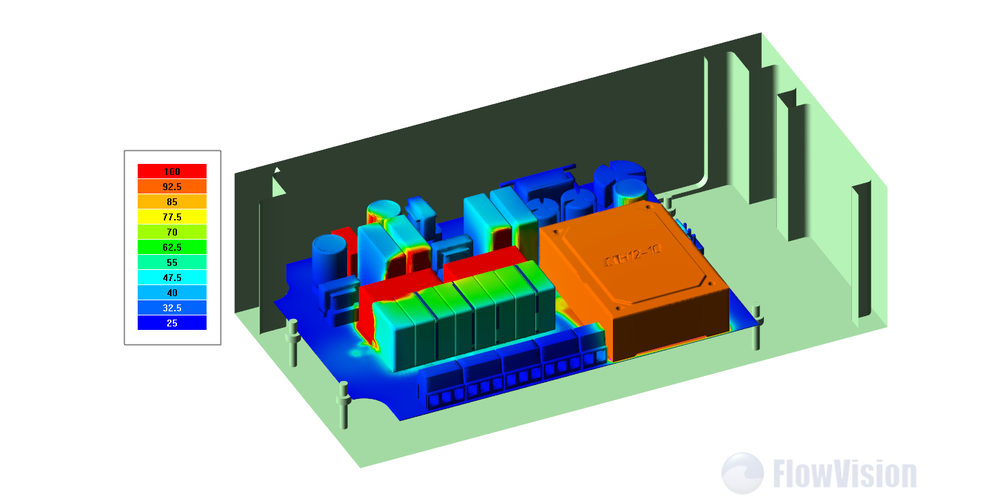
- Теплообмен внутри электронных приборов. В частности, на рисунке 1 (в заглавии статьи) представлены результаты моделирования физических процессов, протекающих в радиоэлектронном блоке;
- Процессы, протекающие в турбинах или ракетных двигателях;
- Различные камеры сгорания.
FlowVision имеет множество возможностей для моделирования подобных процессов. В рамках данной статьи проводится сравнение результатов расчетов с применением традиционных моделей излучения (подробное описание моделей в документации), которые реализованы в FlowVision и описаны далее в статье, и с применением закона Стефана-Больцмана без использования моделей излучения.
В версии FlowVision 3.15.01 была реализована возможность моделирования отвода тепла с поверхности с помощью закона Стефана-Больцмана без включения моделей излучения. Данная постановка применяется только для сопряженных задач, поскольку отвод тепла с помощью данной опции можно настроить только на граничных связях для связанных граничных условий, также такую постановку целесообразно применять в задачах, где можно не учитывать отвод тепла в сплошную среду.
Тепловой поток по закону Стефана-Больцмана рассчитывается как:
где ε – степень черноты поверхности; T04 – температура окружающей среды [K]; Tsurf – температура поверхности [K]; σ – постоянная Стефана-Больцмана, равная 5,67·10-8 [Вт·м-2·K-4].
Стоит отметить, что вариант расчета с использованием закона Стефана-Больцмана значительно экономит вычислительные ресурсы по сравнению с постановками, в которых используются традиционные модели излучения. В то же время, полноценные расчетные модели излучения позволяют учесть процесс взаимодействия излучения с веществом среды, особенно данный процесс существенен при высоких температурах (порядка тысячи градусов), но такое взаимодействие невозможно смоделировать, используя только закон Стефана-Больцмана.
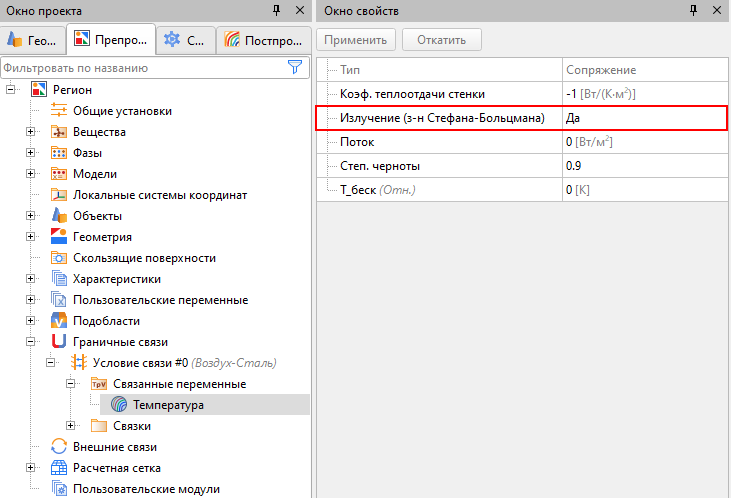
На рисунке 2 показано то, как настраивается отвод тепла с поверхности за счет излучения по закону Стефана-Больцмана в окне свойств условий связи, в этом же окне задается степень черноты тела (Дополнительную информацию можно получить из документации).
Рисунок 2 – Задание излучения по закону Стефана-Больцмана
В рамках сравнительного исследования моделировался процесс охлаждения воздухом металлического бруска, в котором задано объемное тепловыделение. Рассматривались следующие постановки:
- С применением модели МДО (метод дискретных ординат);
- С применением модели P1;
- Без применения моделей излучения, с подключением закона Стефана-Больцмана в условиях связи.
Особенности модели P1 и область применения данной модели уже рассматривались в статье «О моделях излучения во FlowVision».
Модель излучения МДО является наиболее комплексной моделью переноса излучения. Данная модель охватывает весь диапазон оптических толщин и позволяет решать такие задачи, как:
- перенос излучения от поверхности за счет передачи тепла через среду;
- учет излучения в задачах горения;
- перенос излучения в полупрозрачных средах (горение в сажевых или пылевых средах).
При использовании данной модели, точность решения и количество решаемых уравнений зависят от количества N дискретных телесных углов Ωi, на которое разбито пространство. Требования МДО к вычислительным ресурсам – умеренные для типичных дискретизаций, однако при большом числе телесных углов потребуются значительные вычислительные мощности.
При использовании закона Стефана-Больцмана необходимо связать граничные условия для получения граничной связи, а затем задать в физических процессах фазы теплоперенос (в рассматриваемой задаче теплоперенос через h) и движение (в рассматриваемой задаче модель Навье-Стокса), после чего подключить данную функцию в окне свойств связанных переменных.
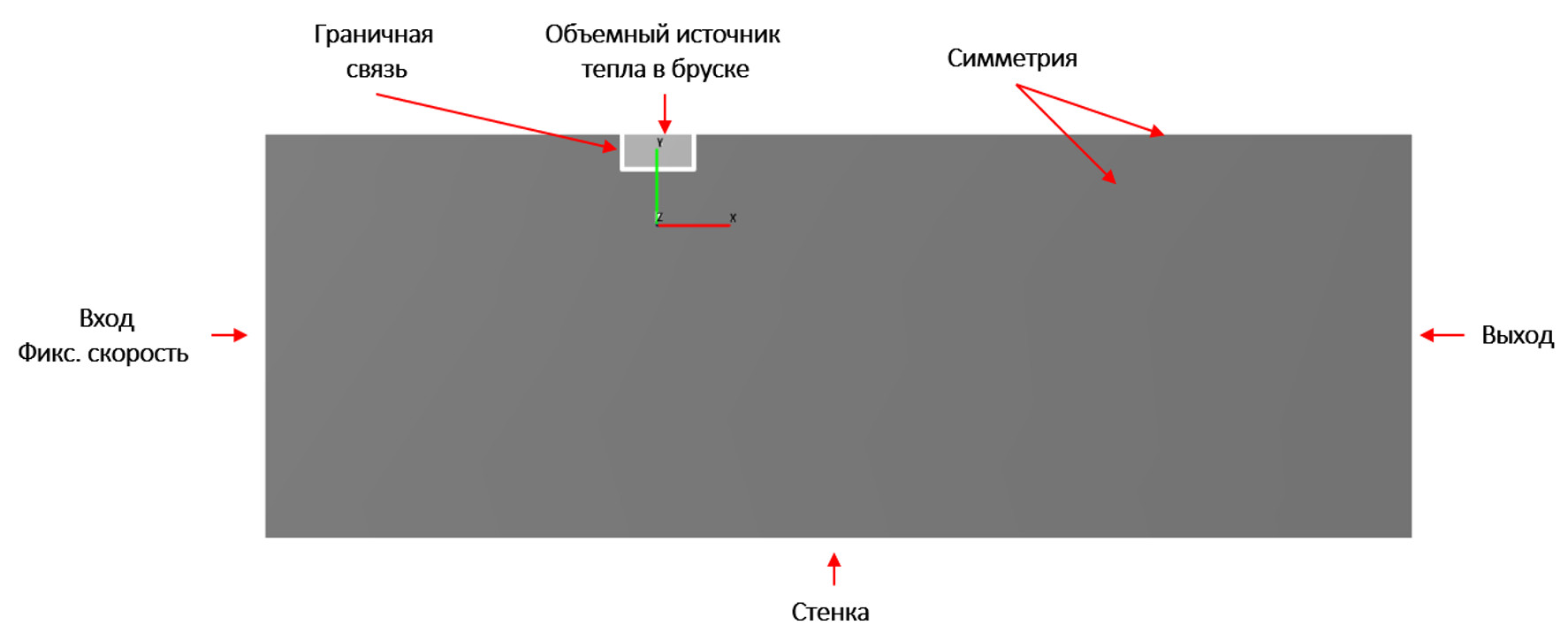
Процесс, на примере которого проводилось сравнение, моделировался в плоской 2D постановке и рассматривалась замкнутая полубесконечная область, чтобы исключить влияние граничных условий входа и выхода на излучение. В задаче присутствует две подобласти (подобласть бруска и подобласть окружающего воздуха), на рисунке 3 представлена схема с граничными условиями для исследуемой задачи.
Рисунок 3 – Расстановка граничных условий
Объемный источник тепла задавался с тепловыделением в 40 кВт/м3, скорость воздуха на входе в расчетную область задавалась равной 0,1 м/c. На стенке расчетной области для разных моделей задавались следующие граничные условия:
- Для модели МДО: Интенсивность излучения – Прозрачная стенка, Температура = 0 K;
- Для модели P1: Плотность излучения – Расчет плотности потока излучения, Температура = 0 K;
В окне свойств модели излучения для P1 задавались следующие настройки:
- Показатель преломления: 1
- Коэффициент релаксации: 0.2
- Коэффициент поглощения: 1e-10 м-1.
Для модели МДО задавались настройки аналогичные настройкам P1, а параметр «Количество Полярных Углов», доступный только для МДО, задавался равным 6.
Начальная расчетная сетка однородная и имеет 100 ячеек вдоль оси X и 50 вдоль оси Y. Задана адаптация вдоль стенки бруска для обеих подобластей со следующими параметрами:
Макс. уровень N: 3
Слоев уровня N: 12
Слоев уровня N-1: 7
Слоев уровня N-2: 7.
На рисунке 4 показано сечение расчетной сетки. При этом количество расчетных ячеек составило 9039, а минимальный размер ячейки – 2 мм.
Рисунок 4 – Сечение расчетной сетки в области бруска
Расчет проводился в режиме распараллеливания при помощи технологии MPI на 8 процессорах и 6 ядрах. Солвер имеет следующие настройки:
- Шаг по времени:
Способ: Числом CFL
Конвективное CFL: 100
Макс. шаг: 0.5 с
- Интегрирование по времени:
Метод: Стационарный (особенности методов интегрирования подробно описаны в документации)
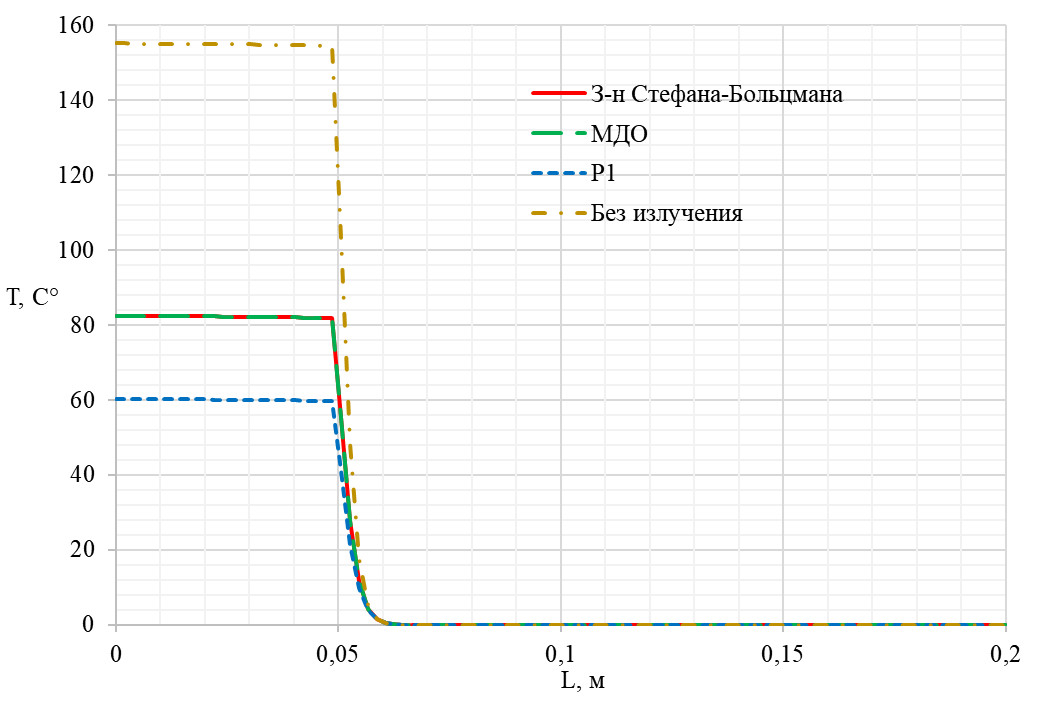
На рисунке 5 представлен сравнительный график распределения температуры вдоль линии, исходящей из центра бруска и проведенной через середину бруска (совпадает с осью Y на рисунке 2).
Рисунок 5 – График распределения температуры вдоль координаты X для разных постановок
Для оценки целесообразности использования моделей излучения в рамках данной задачи также был проведен расчет без какого-либо расчета излучения. Наблюдается отклонение результатов, полученных в постановке с моделью P1, от других постановок. Это объясняется границами применимости данной модели, в частности в модели не предусмотрен сток радиационной энергии и излучение энергии в «бесконечность» невозможно. Модель P1 традиционно используется в замкнутых объемах (подробный пример использования в нашей статье: «Туториал: Электрическая сборка») и в задачах, схожих с задачами внешнего обтекания, может давать отклонения результатов расчета по сравнению с результатами, полученными с применением более требовательной к вычислительным ресурсам моделью МДО. Результаты, полученные в постановке с использованием закона Стефана-Больцмана, совпадают с результатами, полученными в постановке с моделью МДО.
На рисунке 6 представлено сравнение температурных полей для различных вариантов постановок.
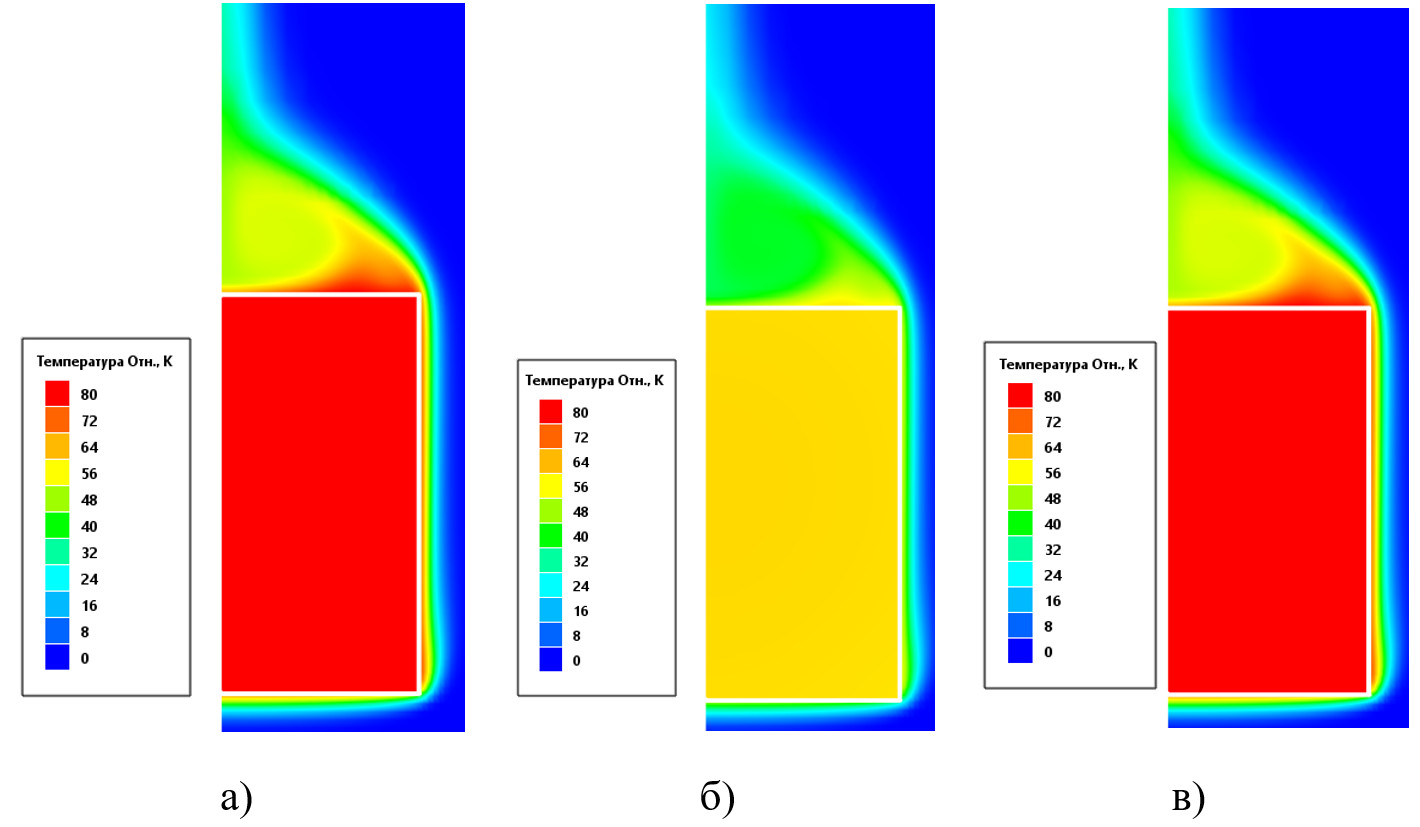
Рисунок 6 – Сравнение температурных полей при использовании: а) Модели МДО б) Модели P1 в) З-на Стефана-Больцмана
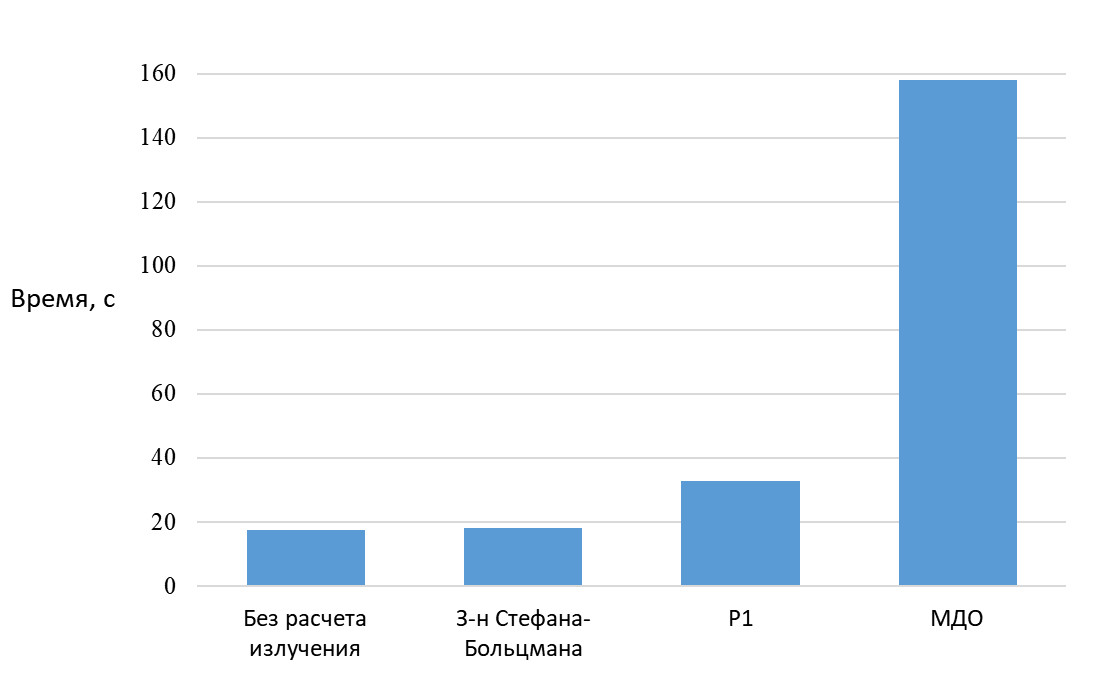
На рисунке 7 представлена сравнительная гистограмма затраченного на расчет времени для каждой постановки.
Рисунок 7 – Сравнительная гистограмма затраченного на расчет времени
Из сравнительной гистограммы видно, что наиболее требовательной оказалась модель МДО, а расчет с использованием закона Стефана-Больцмана занял практически столько же времени, как постановка без расчета излучения.
Таким образом, расчет с подключением закона Стефана-Больцмана и без использования традиционных моделей излучения демонстрирует намного меньшие вычислительные затраты при хорошей точности относительно расчетов с использованием полноценных моделей излучения. Использование данной функции является эффективным и целесообразным, особенно в условиях ограниченных вычислительных мощностей.