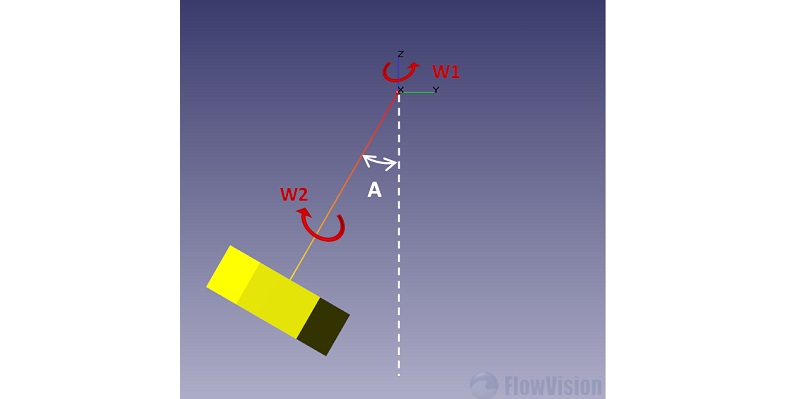
Существует большое количество расчетных задач, которые моделируют явления, происходящие в различных вращающихся агрегатах или около них. При постановке подобной численной задачи важно выбрать способ описания вращения в численной модели, который будет корректен с точки зрения физики и оптимален с точки зрения производительности вычислений. FlowVision позволяет задавать вращение различными способами: с помощью вращающейся локальной системы координат; с помощью подвижных тел; с помощью скользящих поверхностей. С целью помочь пользователю разобраться с постановкой такого типа задач, рассмотрены примеры задач разного типа, начиная с физико-математических основ.
1. Кинематика вращательного движения
1.1. Вращательное движение материальной точки
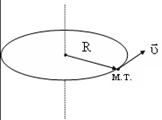
Вращательное движение материальной точки (м.т.) вокруг неподвижной оси – это движение материальной точки по окружности радиуса R, центр которой лежит на неподвижной относительно данной системы отсчета прямой (ось вращения), перпендикулярной плоскости, в которой лежит траектория точки.
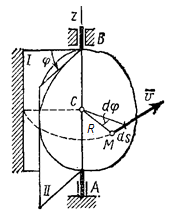
Вращательное движение тела вокруг неподвижной оси - движение тела, при котором все его точки, двигаясь в параллельных плоскостях, описывают окружности с центрами, лежащими на одной неподвижной прямой, называемой осью вращения. Тело, совершающее вращательное движение, имеет одну степень свободы, и его положение относительно данной системы отсчёта определяется углом поворота φ между неподвижной полуплоскостью и полуплоскостью, жёстко связанной с телом, проведёнными через ось вращения.
1.2. Угол поворота
Угол φ считается положительным, если он отложен от неподвижной плоскости в направлении против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца оси Az), и отрицательным, если по ходу часовой стрелки. Чтобы знать положение в любой момент времени, надо знать зависимость угла φ от времени t, т.е. φ=f(t).
1.3. Основные кинематические характеристики вращательного движения
Основными кинематическими характеристиками вращательного движения являются угловая скорость ![]() и угловое ускорение
и угловое ускорение ![]() .
.
Угловая скорость и угловое ускорение величины векторные. Вектор угловой скорости направлен вдоль оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки (рис.3). Такой вектор определяет сразу и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси. Аналогично углу поворота, когда вращение происходит против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца оси Az) ω>0, а когда по ходу часовой стрелки, то ω<0. Таким образом, знак ωопределяет направление вращения. 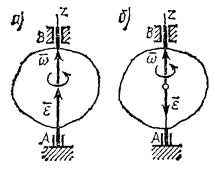 а)
а) 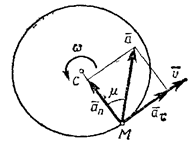 б)
б) 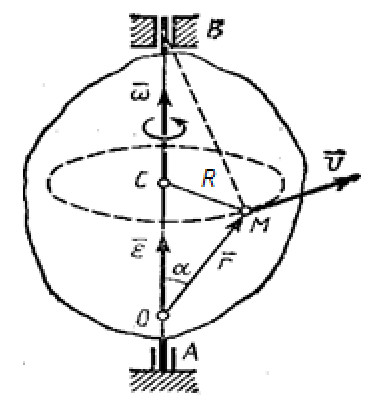 в)
в)
Рис.3
1.4. Прочие кинематические характеристики
Скорость точки M на расстоянии R от оси (рис.2): ![]()
Тангенциальная составляющая ускорения точки M (рис.3б): ![]()
Нормальная составляющая ускорения точки M (рис.3б): ![]()
Полное ускорение точки M (рис.3б): ![]()
2. Силы инерции, действующие на материальную точку во вращающейся системе отсчета
2.1. Материальная точка, покоящаяся во вращающейся системе отсчета
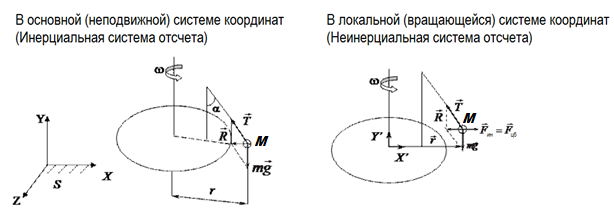
Если рассмотреть движение вращающейся точки M, то относительно неподвижной системы координат (СК) XYZ (рис.4а) силу, действующую на неё можно определить из второго закона Ньютона: ![]() . Относительно вращающейся системы координат X’Y’Z’ точка M неподвижна (рис.4б). Это обеспечивается тем, что равнодействующая сил уравновешивается инерциальной силой (центробежной):
. Относительно вращающейся системы координат X’Y’Z’ точка M неподвижна (рис.4б). Это обеспечивается тем, что равнодействующая сил уравновешивается инерциальной силой (центробежной): ![]() .
.
2.2. Материальная точка, движущаяся во вращающейся системе отсчета
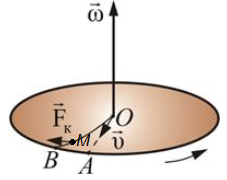
Если же точка движется во вращающейся системе отсчета, то помимо центробежной силы на неё действует ещё одна сила инерции – сила Кориолиса ![]() (рис.5). Направление силы Кориолиса определяется правилом правого винта.
(рис.5). Направление силы Кориолиса определяется правилом правого винта.
Таким образом, при переходе от основной неподвижной СК к локальной СК, которая является вращающейся системой отсчета, появляются дополнительные составляющие вектора силы, которые действуют на материальную точку: центробежная сила ![]() и сила Кориолиса
и сила Кориолиса ![]() .
.