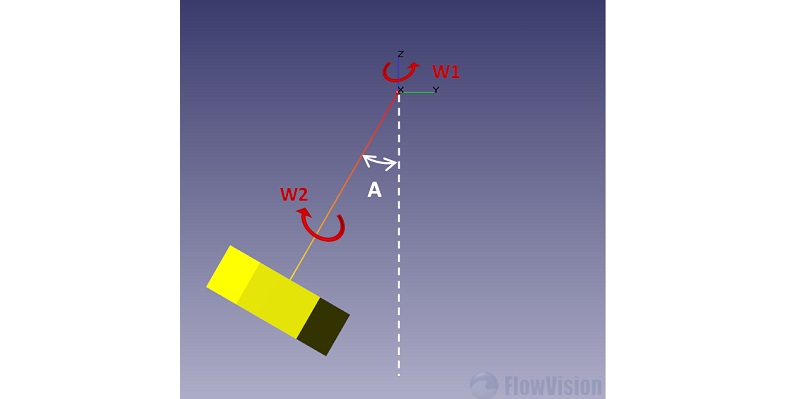
3. Задание вращения во FlowVision
В данном разделе рассматривается элементы дерева проекта в ПреПроцессоре FlowVision, в которых могут быть заданы параметры, определяющие вращение.
3.1. Задание параметров, определяющих вращение для локальной системы координат
3.1.1. Задание самой локальной системы координат (ЛСК)
Локальные системы координат-> Локальная СК #
- Начало: задаются координаты начала ЛСК в глобальной системе координат
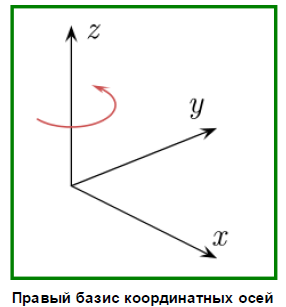
- Оси: задаются значения проекций направляющих векторов осей X и Y локальной системы координат на оси глобальной системы координат. При этом не обязательно вводить нормированные значения, программа автоматически нормирует их. При вводе данных для одной из осей, например X , программа автоматически корректирует значения для второй оси. Ввод данных для оси Z вообще не предусмотрен - она строится автоматически по данным, введенным для осей X и Y таким образом, чтобы она была перпендикулярна осям X и Y и образовывала бы с ними правый базис (рис.6.).
Рис. 6.
3.1.2. Задание вращения в ЛСК
Локальные системы координат-> Локальная СК # ->Вращение->Вращение #
- Скорость: Задается угловая скорость вращения ω, в рад/с (с-1)
- Центр: Задается положение центра вращения в локальной системе координат
- Направление: Задаются проекции направляющего вектора оси вращения на оси ЛСК. При этом не обязательно вводить нормированные значения, программа автоматически нормирует их.
3.2. Задание вращения на регионе
При задании на Регион локальной системы координат и вращения, задача переводится во вращающуюся систему отсчета. При этом согласно п.2 на вещества в расчетной области, действует центробежная сила 
и сила Кориолиса 
. Уравнение Навье-Стокса дополняется соответствующими составляющими: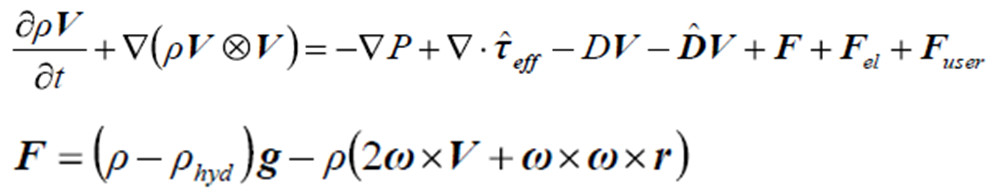
Для корректной постановки задачи, внешние границы Региона должны быть поверхностями вращения или связанным ГУ с назначенным периодическим условием связи (рис. 7).
Рис. 7.
Граничные условия по умолчанию остаются заданными в глобальной системе координат. Поэтому для нужных ГУ (поверхности, которые вращаются в глобальной системе координат) необходимо задать вращение (см. 3.4.).
3.3. Задание вращения на граничном условии
При задании вращения на ГУ подразумевается добавление к скорости поверхности, заданной в Граничном условии 
, дополнительной тангенциальной составляющей 
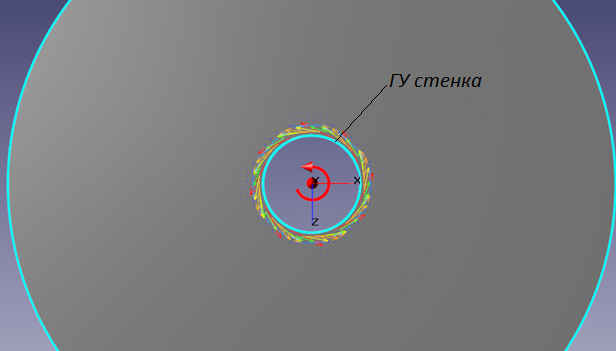
, тогда вектор скорости данной точки границы можно определить как 
. На рис.8 представлен пример при задании вращения на ГУ Стенка: трение на стенке увлекает поток в попутном направлении.
Рис. 8.
На рис.9 представлен пример, в котором на ГУ Вход/Выход задано вращение и нормальная массовая скорость, поэтому результирующие вектора скорости направлены под углом к соответствующим нормалям окружности. Поверхность ГУ, на котором задается вращения не обязательно должна являться поверхностью вращения.
Рис. 9.
3.4. Задание вращения на регионе и граничном условии
В случае задания на Регионе ЛСК и Вращения мы рассматриваем движение в относительной системе координат, значит добавляем в расчет центробежную и Кореолисову силы, а задавая ЛСК и Вращение на ГУ мы добавляем тангенциальную составляющую скорости на поверхностях этого ГУ. Таким образом, для решения задачи в локальной системе координат вращающихся поверхностей (например ротора), необходимо задание ЛСК+Вращение на Регионе, а так же задание ЛСК+Вращение на тех ГУ, поверхности которых так же вращаются относительно глобальной системы координат. На всех остальных поверхностях (неподвижных в глобальной системе координат) ничего задавать не нужно. Поверхности, которые неподвижны в глобальной системе координат, включая внешние границы региона должны быть поверхностями вращения, а «вращающиеся» поверхности могут быть любыми.
3.5. Задание вращения на подобласти
Вращение на подобласти (ЛСК и Вращение) задается в случае использования «скользящей поверхности» для той подобласти, в которой будет использована вращающаяся система координат. При этом, как и в случае задания вращения на регионе согласно п.3.2 на вещества в этой подобласти, действует центробежная сила и сила Кориолиса и уравнение Навье-Стокса дополняется соответствующими составляющими (см. п.3.2).
3.6. Задание вращение для модификатора «Подвижное тело»
Для подвижного тела может быть задан любой вид движения, в том числе и вращение.
Вращение здесь задается проекциями вектора угловой скорости на оси глобальной (абсолютной) системы координат (ωx, ωy, ωz) , а центр вращения задается либо совпадающим с центром инерции, либо координатами в локальной системе координат объекта.
4. Отображение результатов
FlowVision отображает скорость и другие векторные переменные в спутной системе координат. Это – глобальная (абсолютная) СК, совпадающая в данный момент времени с локальной (относительной) СК.
Поэтому пользователь видит геометрическую модель расчетной области в локальной (относительной) СК, а векторные переменные — в абсолютной СК (Рис. 10.). Однако для векторов существует также возможность отображения в относительной СК (Рис. 10.). Для этого необходимо задать параметры необходимой системы отсчёта в свойствах слоя «Векторы» в разделе Движущаяся СК.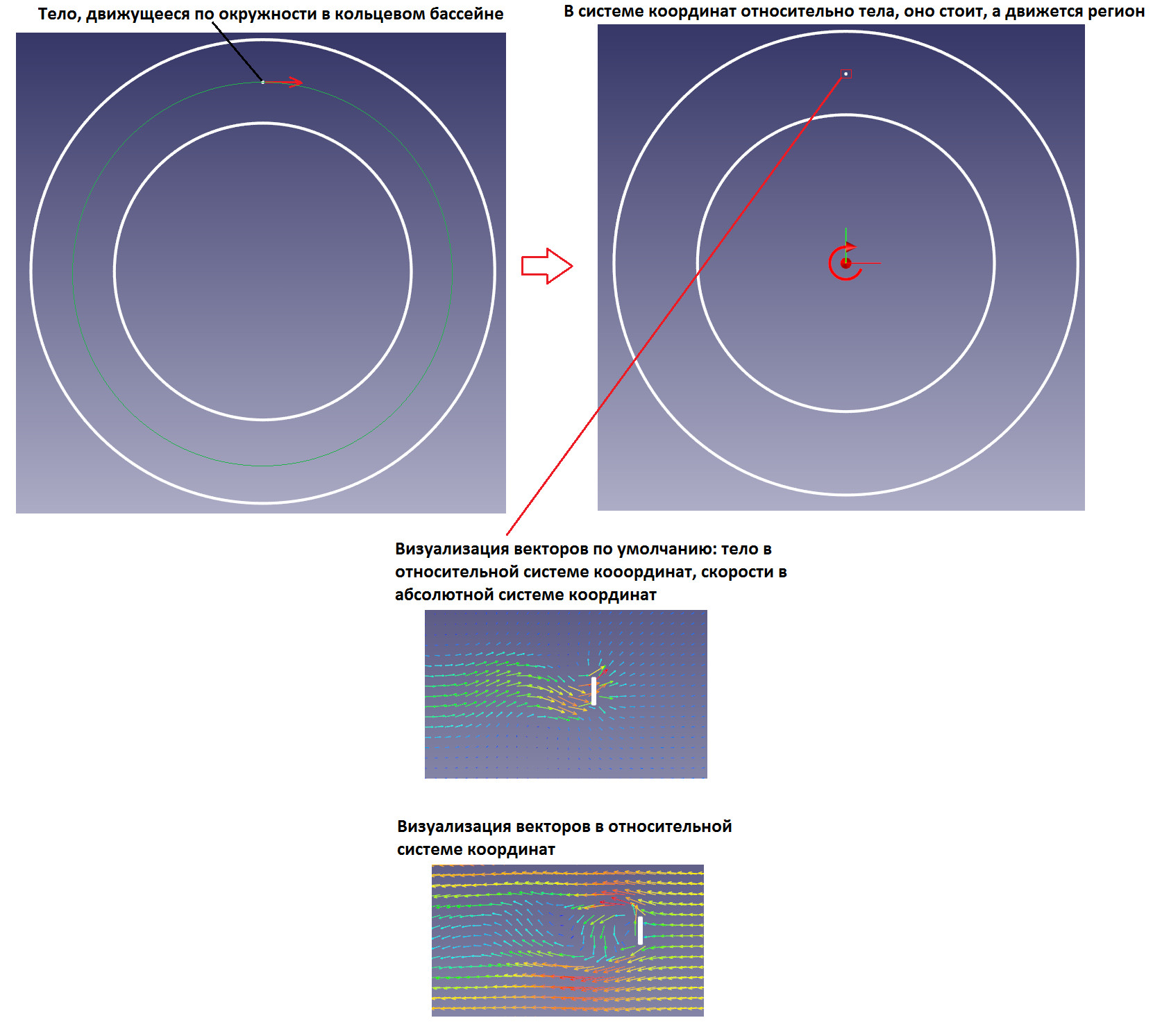
Рис. 10.