Результаты расчётов в первой части исследования аэродинамики тела Ахмеда оказались не самыми точными: погрешность составила 12%. Но в прошлый раз расчёты проводились на грубой сетке, которая не соответствовала Y+, найденному в результате исследования сходимости. Если бы мы обеспечили требуемый Y+, то расчёт на такой подробной сетке длился бы месяцами или же потребовал больших вычислительных мощностей.
Для повышения точности было решено продолжить разработку методики.
Напомню, что мы пытаемся повторить эксперимент Ахмеда во FlowVision. В первой части нашего исследования для 3D расчёта расчётную сетка адаптировалась только по поверхности тела и за ним. Однако точность полученных результатов оставляла желать лучшего. Сейчас мы постарались сэкономить и повысить точность: применили локальную адаптацию в стратегически важных местах.
Забегая вперёд, выделим структуру текущего исследования:
- Анализ влияния сил трения
- Модернизированное исследование сходимости по сетке
- Расчёт 3D постановки
- Анализ подъёмной силы
Анализ влияния сил трения
При расчёте течений, для которых возникают зоны хоть и незначительного отрывного течения, важно предельно точно учитывать влияние силы вязкого трения. Под действием трения точка отрыва потока смещается - из-за этого возникает существенная погрешность в расчёте аэродинамических характеристик (АДХ) модели.
Если влияние силы трения велико, то для разрешения тонкого вязкого подслоя используется LES подход (для FV он реализован в функционале OBL). Если не использовать LES подход, то необходимо разрешать сеткой все структуры потока: зоны отрыва и присоединения потока, вихрей и т.д.
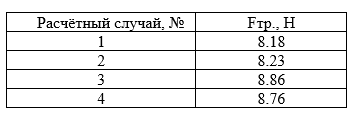
Сила трения определялась как характеристика "Касательное напряжение", построенная на модели. Результаты для случаев при использовании рассмотренных в прошлой статье 4-х вариантов адаптации приведены в таблице. Напомню - адаптация проводилась в объёмах параллелепипедов вокруг и за телом.
Рассмотренные варианты адаптации сетки
1. 
2.
3.
4.
Таблица 1. Величина силы трения в зависимости от расчётного случая
Результаты, полученные при измельчении сетки в вихревой зоне не сильно отличаются друг от друга.
Это позволяет предположить, что силы трения не вносят существенный вклад. Поэтому использование OBL для данного расчёта не требуется.
Модернизированное исследование сходимости
Так как точность проведённых расчётов нас не устроила, необходимо было искать другие способы улучшения расчётной сетки - адаптации в характерных для данного обтекания областях. Проще и быстрее искать необходимый набор адаптаций в 2D постановке.
В 2D исследовании сходимости по сетке (из первой части исследования) мы получили силу равную Fx= 0.44 Н. Мы начали расчёты с этой сеткой в 3D постановке и уперлись в ограничитель по вычислительным ресурсам. Поэтому пришлось адаптировать сетку не по всей поверхности тела (как при исследовании сходимости по сетке), а только части за скосом - мы предположили, что это самое важное место, определяющее величину Сх. Теперь снова начнем 2D модернизацию сетки и будем стремиться к получению результатов из исследования сходимости в размере величины Fх = 0,44 Н.
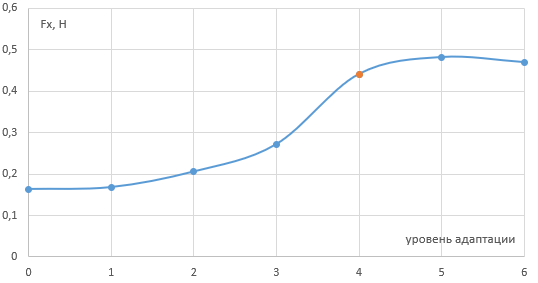Рисунок 1 - 2D исследование сходимости по сетке (из первой части)
Расчёт №1
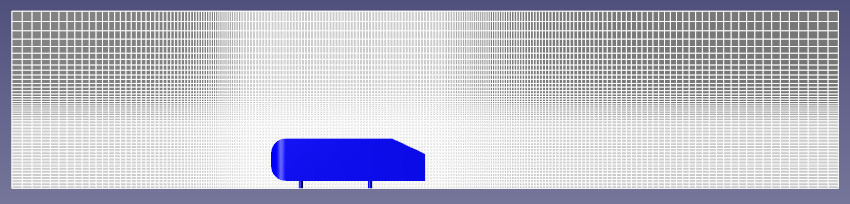
Начнём с конфигурации адаптации 3D сетки, на которой остановились в прошлый раз. Измельчим сетку вокруг тела Ахмеда (1) и локально вблизи скошенной поверхности (2). В 3D расчёте мы так и не стали использовать сетку полученную при исследовании сходимости по сетке (2-ым уровнем в объёме параллелепипеда и 4-ым уровнем по поверхности тела) из-за нехватки вычислительных ресурсов и использовали адаптацию по мере возможностей компьютера
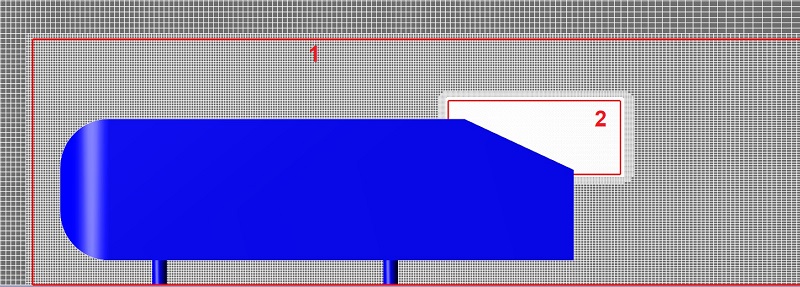
Рисунок 2 - расчётная сетка в 2D постановке: адаптация из прошлого расчёта
Таблица 2. Результаты (расчёт №1)
Величина продольной силы (Fx) далека от полученного при сходимости по сетке (Fx = 0.44 Н). Однако в этот момент стоит задаться вопросом: почему адаптация скоса в первой части статьи позволила приблизится к эксперименту с точностью в 1,2% (для φ = 25 º)? Ответ был найден при пристальном рассмотрении результатов нашего самого первого расчёта - 2D исследования сходимости по сетке.
Возвращаясь назад
Исследование сходимости по сетке (из первой части)
Проводилась последовательная адаптация сетки в параллелепипеде и на поверхности модели. Для каждой сетки определялась величина силы лобового сопротивления Fx. Сходимость достигается тогда, когда величина Fx перестаёт зависеть от изменения размера ячейки.
На рисунках ниже изображены расчётная сетка: максимальный уровень адаптации = 6 и сами результаты исследования сходимости по сетке. Разница между величинами сил лобового сопротивления для 4 и 6 уровня составила меньше 10%, а экономия расчётной сетки - в 4 раза. Поэтому для дальнейшего решения этой задачи был выбран 4 уровень адаптации расчётной сетки.
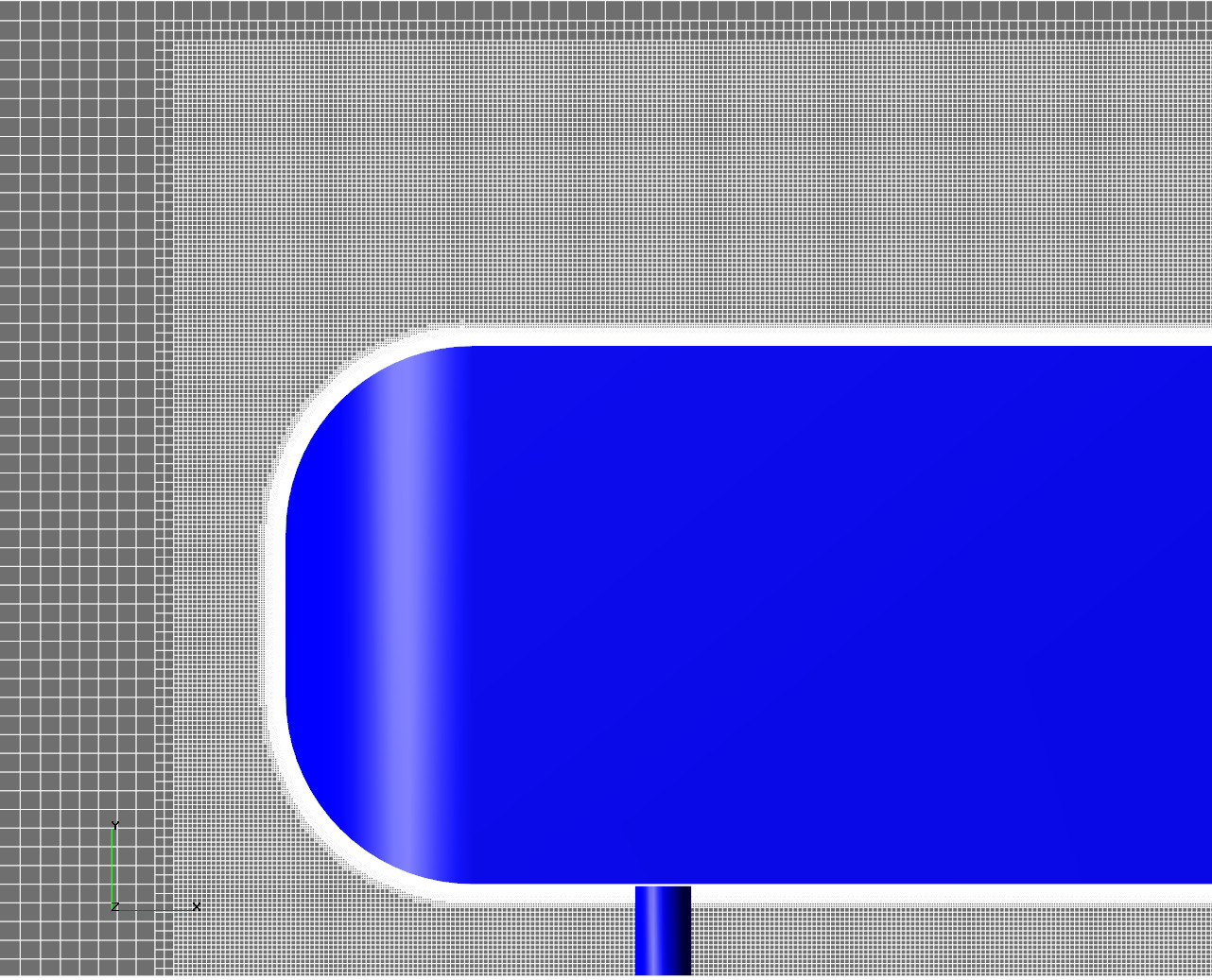
Рассматривая слои скорости в расчётах по исследованию сходимости по сетке (для 3 - 6 уровней), замечаем, что при увеличении уровня адаптации (измельчении размера ячейки) точка отрыва на скошенной поверхности значительно перемещается. Именно из-за этого перемещения происходит перераспределение давления на поверхности и, аэродинамическая сила изменяется.
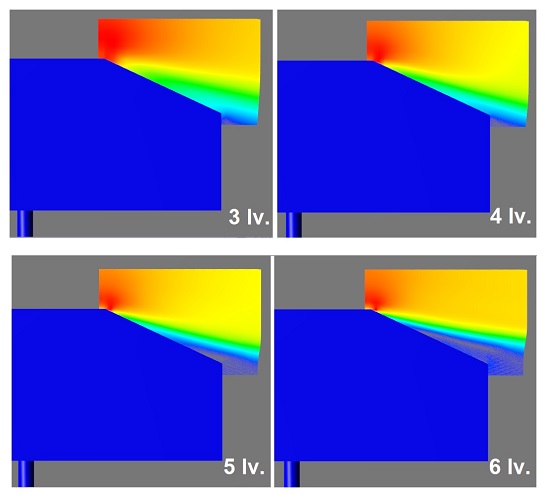Рисунок 3 - Перемещение точки отрыва при увеличении уровня адаптации при 2D исследовании сходимости по сетке
Важно разрешать не только область вблизи скоса, но и отдельно саму поверхность скоса. Это обеспечит более правильное положение точки отрыва.
Расчёт №2
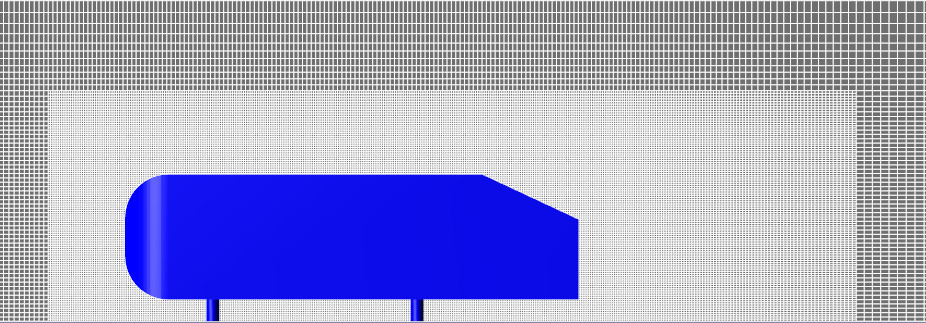
Вместо параллелепипеда за скосом будем измельчать сетку непосредственно вблизи скошенной поверхности.
Рисунок 4 - расчётная сетка в 2D постановке: адаптация 4 уровнем по поверхности скоса
Таблица 3. Результаты (расчёт №2)
Мы приблизились к величине продольной силы, полученной ранее на сходимости (Fx = 0,44 Н) - но всё ещё далеко. Исследуя распределение давления, замечаем странную вещь - в точке разворота потока (при обтекании верхней поверхности и переходе на скошенную) присутствует странное разряжение.
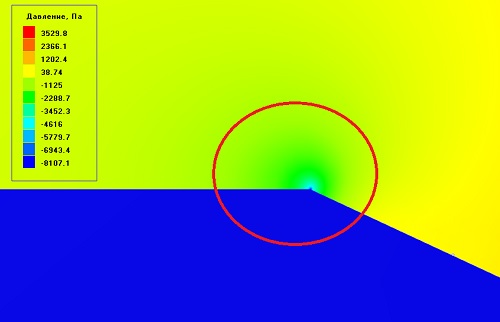Рисунок 5 - Визуализация слоя давление (сверху) и разрежение на уступе (снизу)
Расчёт №3 2D - финальный
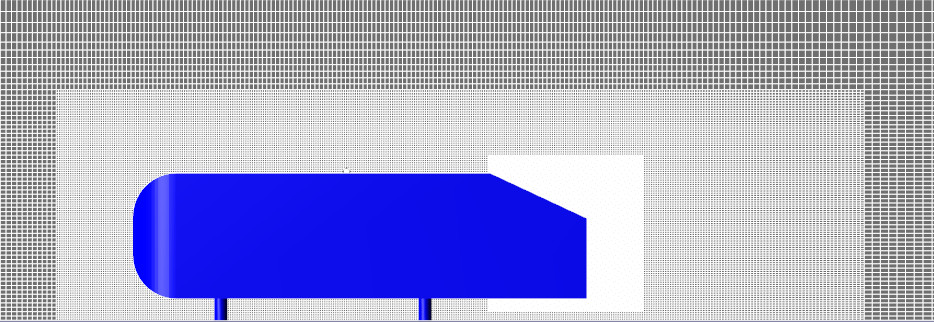
Принимается решение дополнительно проадаптировать этот угол с помощью адаптации острых кромок. (Хорошо, что во FlowVision есть такой функционал!) Применим к лобовой поверхности тела адаптацию по кривизне, чтобы дополнительно разрешить область торможения потока.
Рисунок 6 - Расчётная сетка с адаптацией по кривизне и острым граням
Таблица 4. Результаты (расчёт №3)
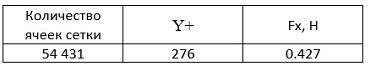
Мы приблизились к величине продольной силы при исследовании сходимости (Fx = 0.44 Н) с точностью 3%.
Таблица 5. Сравнение результатов (расчёт №3 и исследование сходимости (ИС))
Разрежения в слое давление пропали.
Рисунок 7 - Визуализация слоя давление (расчёт №3)
3D расчёт
Перенесём модернизированную сетку из 2D расчёта на 3D. Количество ячеек трёхмерной сетки составило порядка 9 800 000 ячеек.
Это в два 2 раза меньше, чем было при первой попытке запустить 3D расчёт с найденной сходимостью по сетке.
Работа выполнена с использованием оборудования Центра коллективного пользования сверхвысокопроизводительными вычислительными ресурсами МГУ имени М.В. Ломоносова. На этот раз все расчётные случаи посчитались на кластере за неделю. Для расчёта использовалось 4 процессоров по 86 ядер. И результаты не могут не радовать, смотрим на результаты расчёта коэффициента сопротивления для разных углов и сравниваемся с экспериментом!
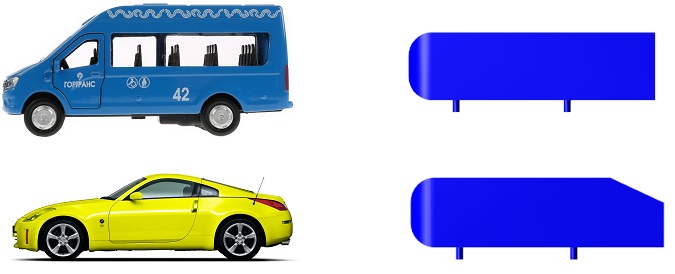
Геометрия моделей с разным углом скоса
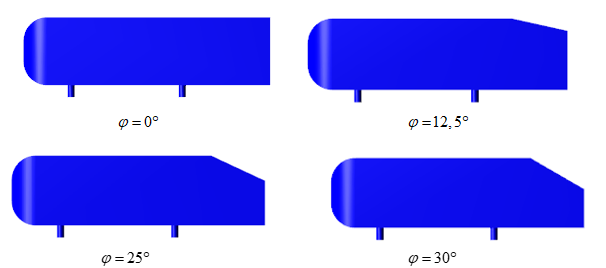
При сравнении с результатами, полученными Ахмедом, максимальная погрешность составляет 5%.
Таблица 6. Сравнение с экспериментом Ахмеда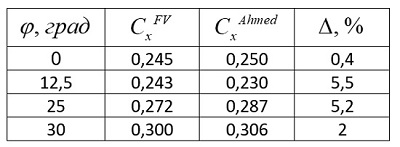
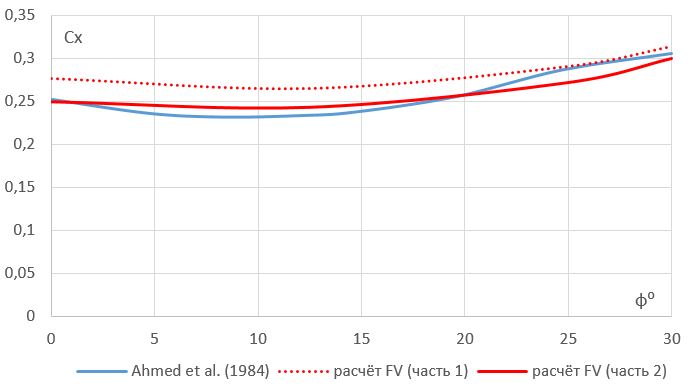
Для наглядности данные из таблицы 6 отражены на графике. Раньше мы были дальше от эксперимента Ахмеда, теперь точность расчёта заметно повысилась.
Рисунок 8 - Сравнительный анализ расчёта Сх во FlowVision и эксперимента Ахмеда
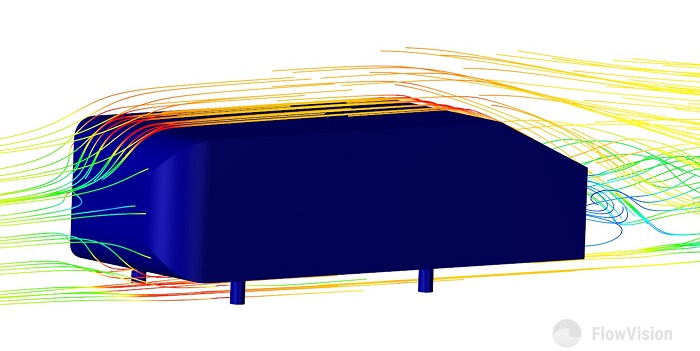
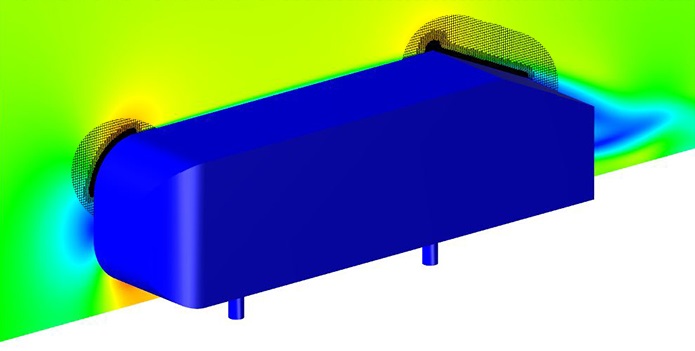
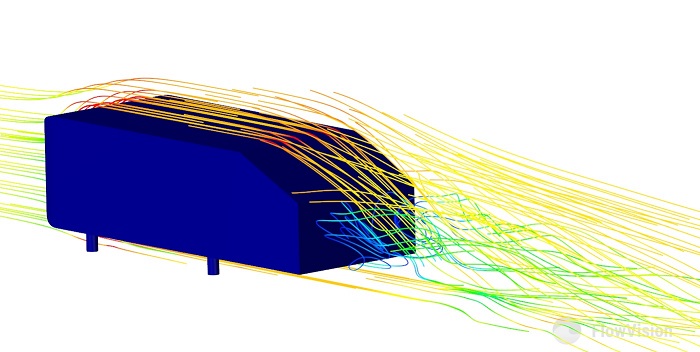Рисунок 9 - Линии тока вблизи поверхности тела Ахмеда
Маленькое отступление о подъёмной силе автомобиля
В настоящее время вектор развития автомобильной аэродинамики изменился. Если раньше при проектировании автомобиля стремились к уменьшению силы лобового сопротивления, то сейчас определяющим фактором является подъёмная (или прижимная) сила.
Воздух, протекающий под автомобилем, тормозится о нижние стенки. А чем ниже скорость, тем выше давление. Давление под автомобилем повышается - и вот мы имеем аналогию с возникновением подъёмной силы у крыла. Поэтому выше скорость набегающего потока, тем сильнее воздух снизу будет поднимать автомобиль. Очевидно, что чем меньше подъёмная сила, тем лучше. Для спорткаров же оперируют понятием прижимной силы (то есть отрицательной подъёмной силой). Рассмотрим на примере тела Ахмеда как изменяется подъёмная сила в зависимости от угла скоса модели.
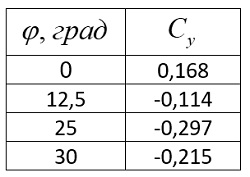
Таблица 7. Результаты расчёта коэффициента подъёмной силы
Представим результаты в виде графика. Если в задней части автомобиля нет скосов, то сила из прижимной становится подъёмной.
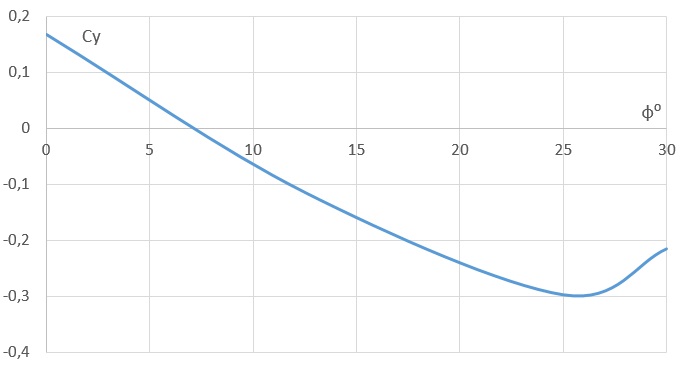Рисунок 10 - Результаты расчёта Сy во FlowVision
Теперь понятно, почему так сильно трясёт в маршрутках - они пытаются взлететь :)
Выводы
Для начала ответим на вопросы, которые были поставлены в конце предыдущей статьи.
- Достаточно ли подробно учитывается вихреобразование в области следа?
Вихреобразование в области следа напрямую зависит от положения точки отрыва на скошенной части. Было замечено, что положение точки отрыва зависит от степени разрешения пристеночного слоя на скосе. Задача исследования сходимости по сетке сводится к разрешению пограничного слоя и нахождению действительного положения точки отрыва. В этом случае вихри за скосом необходимо разрешать, но не так подробно как пристеночный слой. Так как именно правильное положение точки отрыва в большей мере определяет структуру течения в области следа. - Каковы пределы в стремлении сэкономить в количестве ячеек расчётной сетки?
Нам удалось сэкономить расчётную сетку в два раза: количество ячеек для 3D расчёта составило порядка 9,8 млн. ячеек, что существенно сэкономило расчётное время и вычислительные ресурсы. - Будем ли мы применять LES модель к решению?
Нет, LES подход при решении не использовался. Мы определили, что измельчение сетки мало влияет на величину силы трения. - Потребуется ли для данного расчёта кластер?
Да, мы использовали для расчёта кластер. Каждый расчётный случай считался примерно 2 суток на 4 процессорах по 86 ядер.
Делаем выводы: Пренебрегать исследованием сходимости по сетке нельзя. Для экономии ресурсов, её лучше проводить в 2D постановке. В этой работе мы перешли от простой последовательной адаптации в объёме и по поверхности к локальной адаптации только важных мест (определив их предварительно) - тем самым удалось в разы уменьшить количество расчётных ячеек. При помощи "осмысленной" адаптации удалось сократить величину погрешности с экспериментом в 2 раза: теперь это 5%. При этом, количество ячеек сетки позволило нам провести расчёты при адекватной затрате вычислительных ресурсов и в адекватные сроки.
Читайте далее
В следующей статье мы рассмотрим постановку аналогичной задачи в расчётном модуле гидро-газодинамики ПК Kompas от компании АСКОН - Kompas Flow.
Все статьи из цикла: