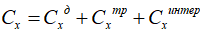Неспадающая актуальность работ по поиску формы оптимального сопротивления в автомобильной отрасли навела нашу команду на мысль:
"можно ли с помощью FlowVision достоверно определить аэродинамические характеристики таких тел?".
Давайте искать ответ вместе!
На примере известной в автомобильной отрасли верификационной задачи мы рассмотрим все этапы моделирования, начиная с постановки.
Тело Ахмеда – стандартная модель для верификации
Первый этап работы заключался в поиске литературы. Так я узнала про тело Ахмеда – модель, геометрически близкую к корпусу автомобиля, которая общепринято применяется для верификации возможностей CFD комплексов в автомобильной промышленности.
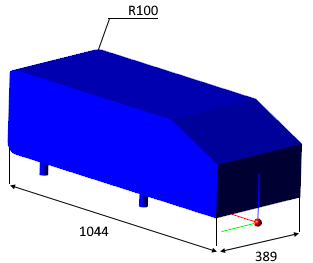
Рис.1. Геометрия тела Ахмеда
Исследуемая модель представляет собой плохообтекаемое тело со скошенной кормовой частью, поднятое над поверхностью земли на 50 мм.
Особенности обтекания тела Ахмеда достаточно подробно освещены в литературе.
Однако первое упоминание связано с исследованиями С.Р. Ахмедом структуры потока, возникающей при движении наземного транспортного средства.
В его работе особый интерес представляло влияние скоса на величину суммарного аэродинамического сопротивления тела.
Результаты эксперимента Ахмеда
Моя цель - сравнить результаты расчёта во FlowVision с экспериментальной зависимостью коэффициента лобового сопротивления (Drag Coefficient) от изменения угла скоса модели (φ).
Определение последовательности исследований
- Определение сходимости решения по сетке и шагу для 2D постановки
- 3D постановка задачи на основе полученных условий
Первые расчёты будут проводиться в 2D постановке. В этом случае без существенных затрат вычислительных ресурсов можно быстро определить сходимость решения по сетке и шагу. Поиск сходимости крайне важен для любой задачи: это единственное условие, гарантирующее Вам достоверный результат.
Отметим, что при проведении поиска сходимости для 2D постановки нельзя опираться на величину исследуемого параметра как на конечные данные. Например, сила лобового сопротивления (Fx , H) будет крайне мала, так как действует она только на площадь продольного сечения, а не на всю поверхность.
И даже при попытке посчитать коэффициент сопротивления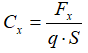 
, он окажется неверным: при обтекании исключено возникновение трёхмерных эффектов течения.
Результаты, полученные в 2D постановке нельзя отмасштабировать на полную геометрию. Однако сетку и шаг, для которых определена сходимость решения, необходимо будет перенести уже на 3D расчёт.
Подготовительный этап (2D постановка)
1. Выбор геометриии плоского расчёта
2. Определение сходимости решения по сетке
3. Определение сходимости решения по шагу
Выбор геометрии для 2D расчёта
На первом этапе численного расчёта необходимо выбрать габариты расчётной области.
В этой задаче отправной точкой стали размеры рабочей части аэродинамической трубы в эксперименте Ахмеда.
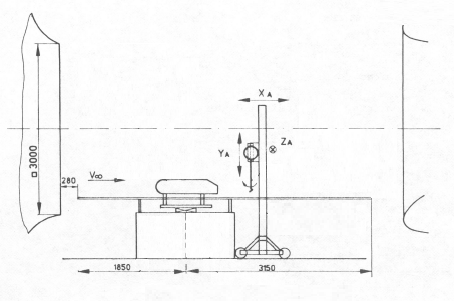
Рис.2. Схема эксперимента Ахмеда
Для 2D проекта были выбраны габариты расчётной области 5.5 х 2.5 х 0,001 м.
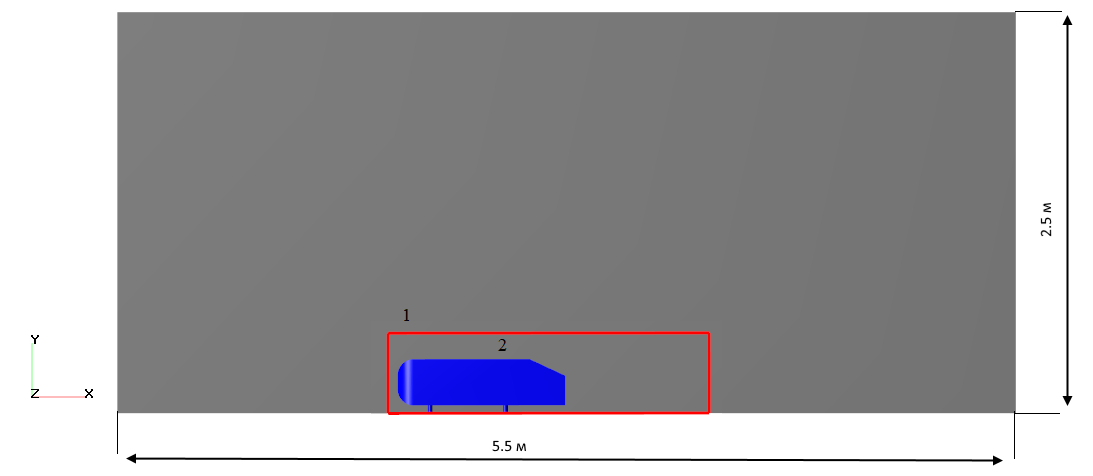Рис.3. Габариты расчётной области
Cходимость по сетке
Начальная сетка была построена неравномерной, со сгущением вблизи обтекаемого тела. Линейный размер минимальной начальной ячейки - 0,01 м.
Далее для выбранной расчётной области начался поиск оптимальной сетки. Проводилась последовательная адаптация сетки в параллелепипеде (1) и на поверхности модели (2). Для каждой сетки определялась величина силы лобового сопротивления Fx. Сходимость достигается тогда, когда величина Fx перестаёт зависеть от изменения размера ячейки.
Рис. 4. Начальная расчётная сетка (уровень адаптации 0)
1 - объект для адаптации области следа
2 - поверхность модели
В ходе этого исследования был достигнут 2 уровень адаптации в параллелепипеде и 6 - на поверхности тела.
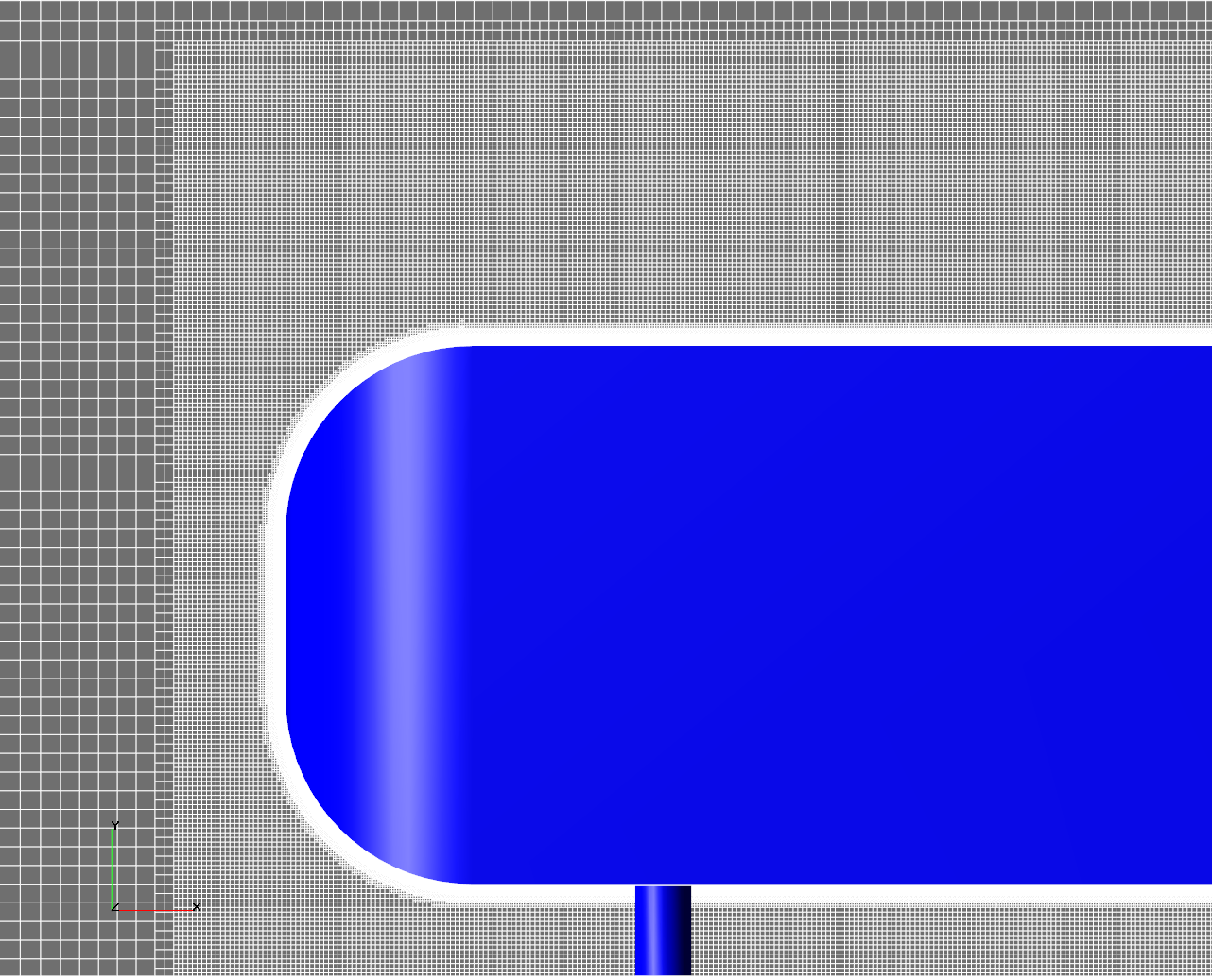Рис. 5. Расчётная сетка (уровень адаптации 6)
При определении сходимости решения по сетке необходимо контролировать следующие параметры:
- количество ячеек - показатель затрат используемых в расчёте вычислительных ресурсов;
- y+ -безразмерный критерий малости ячейки;
- Fx - параметр, по изменению которого определяется сходимость. Это может быть давление / сила / скорость - главное, чтобы изменение этого параметра было характерно для рассматриваемого Вами физического процесса.
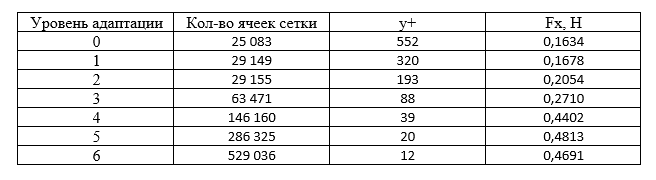
Таблица 1. Результаты сходимости решения (силы лобового сопротивления) по сетке
Результаты таблицы также отражены на графике.
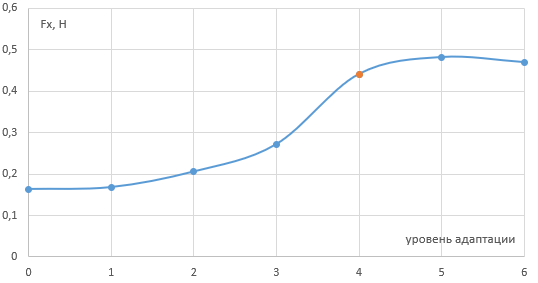Рис. 6. График сходимости решения по сетке
Разница между величинами сил лобового сопротивления для 4 и 6 уровня адаптаций составила меньше 10%, а экономия расчётной сетки - в 4 раза. Поэтому для дальнейшего решения этой задачи был выбран 4 уровень адаптации расчётной сетки.
Cходимость по шагу
Исследование сходимости по шагу началось с шага по времени, заданного с помощью числа CFL = 30. При изменении шага по времени в большую и меньшую сторону оказалось, что мы сразу попали в наилучшее значение: для CFL= 20 изменение величины Fx составило меньше 1%, а вот в случае увеличения (CFL= 40) – больше 10%.
Таблица 2. Результаты сходимости решения (силы лобового сопротивления) по шагу
Выбран шаг CFL=30.
3D Постановка задачи: Будем ли считать на кластере?
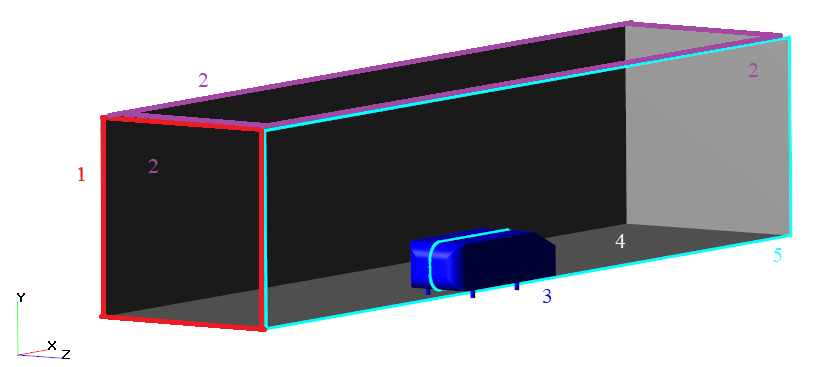
Расчёт объёмной модели производился в симметричной постановке.
Для подобласти с габаритами 5.5 х 2 х 1.2 м заданы стандартные условия атмосферы для вещества (воздух газовая, равновесная) и следующие граничные условия:
1 - Вход, фиксированная скорость V=60 м/с.
2 - Свободный выход с нулевым относительным давлением.
3 - Твёрдая стенка с применением пристеночных функций (равновесие) и шероховатостью.
4 - Твёрдая стенка. Условие для скорости – прилипание.
5 - Симметрия.
В ходе моделирования решаются уравнения движения в форме Навье - Стокса, уравнение энергии с учётом термодинамической энтальпии (h), уравнения неразрывности и состояния.
Замыкание системы осреднённых по числу Рейнольдса (Re) уравнений осуществляется с помощью модели турбулентности SST.
Рис.9. Схема расположения ГУ
Подготовка к расчёту завершена, ничего не предвещает беды. Пробуем применить выбранную нами сетку (4 уровень адаптации, размер ячейки 6,25·10-4) – полученная 3D сетка содержит 19 млн. расчётных ячеек.
Возникает потребность в использовании кластера. Но оптимальная нагрузка одного ядра кластера составляет примерно 20 000 ячеек, а это всего (19 000 000/20 000) 950 ядер!
Ведь это колоссальные вычислительные ресурсы: проект будет бесконечно стоять в очереди, чтобы получить возможность расчёта.
Так дело не пойдёт, включаем всю инженерную смекалку и продолжаем поиски оптимальной сетки.
Теперь уже не будем решать задачу вслепую, а изучим физику исследуемого процесса.
Инженерный подход к решению
Величина коэффициента сопротивления автомобилеподобных моделей складывается из сопротивлений:
- давления, обусловленного воздействием скоростного напора;
- трения, учитывающем вязкостные эффекты;
- интерференционного, обусловленного смешением трёхмерных воздушных потоков вблизи поверхности с образованием вихрей.
Интерференционное сопротивление автомобиля обусловлено наличием выступающих деталей на поверхности кузова. Возмущения, вносимые этими деталями, взаимодействуют с основным воздушным потоком с образованием вихрей.
В нашем случае модель гладкая и влияние интерференционного сопротивления предположительно крайне мало.
Сопротивление давления всего тела можно рассматривать как сумму сопротивлений от отдельных поверхностей: носовой поверхности (front), скошенной (slant) и задней (back). Оставшиеся части модели в эксперименте не участвовали.
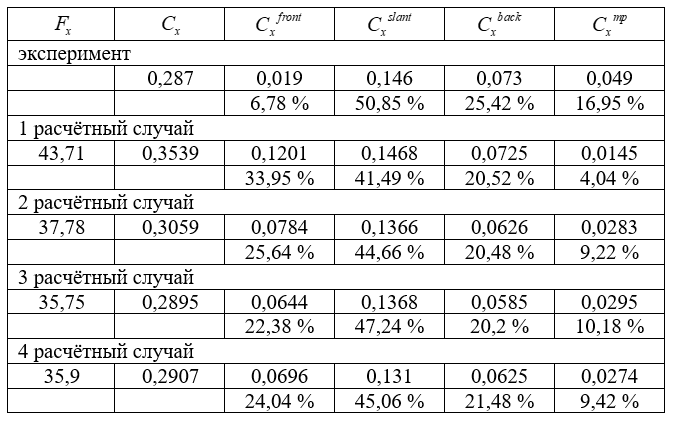
В эксперименте Ахмеда получено не только суммарное значение коэффициента сопротивления при обтекании потоком со скоростью 60 м/с (Сх=0,287), но и вклад от сопротивлений давлений для каждой из поверхностей.
Оставшаяся после вычитания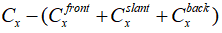 
величина составляет сопротивление трения.
Нельзя пренебрегать заданием шероховатости модели, так как эта величина существенно определяет сопротивление трения.
Таблица 4. Вклад сопротивлений от давления и трения (экспериментальные данные)
В ходе работы был выдвинут ряд предположений о факторах, влияющих на величину коэффициента сопротивления:
-
Влияние отрыва потока с носовой части
Чтобы при моделировании достичь реального положения точки отрыва, требуется обеспечить подход к точке отрыва с определённым градиентом скорости и давления. Точность вычисления этого градиента зависит от степени разрешения сетки области перед носком модели.
-
Влияние вихревой структуры в донной области
Это предположение возникло при попытке уменьшения области адаптации в зоне донного следа – результаты ухудшились. Предположительно, разрешение вихря влияет на величину Cxback.
-
Существенное влияние скошенной части тела
Cопротивление давления от скошенной части, составляет 50% от суммарного сопротивления.
Выбор сетки
Так как сетка, при которой обеспечивалась сходимость решения, требует огромных вычислительных ресурсов, то основной идеей стало определения оптимальной конфигурации адаптации расчётной сетки для получения максимально точного совпадения с экспериментальными данными.
Поиск оптимального набора адаптаций выполнялся по следующему алгоритму:
1. Начальная сетка
Количество ячеек: 286∙73∙66 = 1 325 971
Y+ = 502
Линейный размер пристеночной ячейки: 0,01 м.
2. Адаптация области донного следа 1-ым уровнем адаптации в параллелепипеде с размерами 1,8 х 0,5 х 0,35 м.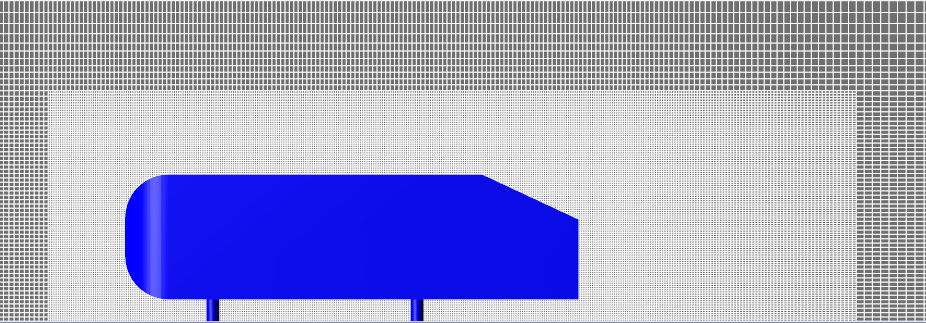
Количество ячеек: 3 248 035
Y+ = 364
Линейный размер пристеночной ячейки: 0,005 м.
3. Адаптация области донного следа 1-ым уровнем + адаптация 2-ым уровнем области вблизи скошенной и задней поверхностей:
Размер параллелепипеда #2: 0,35 х 0,35 х 0,25
Количество ячеек: 4 499 150
Y+ = 317
4. Адаптация области донного следа 1-ым уровнем + адаптация 2-ым уровнем области вблизи скошенной и задней поверхностей:
Размер параллелепипеда #2: 0,35 х 0,15 х 0,22
Количество ячеек: 3 862 714
Y+ = 290
По результатам проведённых расчётов для сетки с разной комбинацией адаптаций была составлена сводная таблица.
Таблица 5. Значения коэффициента сопротивления для разных расчётных сеток
Для 4-го расчётного случая подтверждено предположение о существенном влиянии сопротивления давления от скошенной поверхности тела. Показано, что в этом случае достаточным является адаптация лишь малой области непосредственно над скосом.
Для 3-го расчётного случая рассогласование с экспериментом (Сх=0,287) составляет 0,8%, для 4-го расчётного случая – 1,2%.
Для дальнейших расчётов выбираем 4-ый вариант расчётной сетки.
Выбор модели турбулентности
Мы уже рассказывали о моделировании турбулентности во FlowVision.
Выбор той или иной модели турбулентности может повлиять на результаты численного эксперимента.
Ранее все результаты этой работы были получены для SST модели турбулентности. Для уверенности в правильности выбранной модели проведём ещё один тестовый расчёт.
Для начальной сетки (для упрощения расчёта) заменим SST - модель на KES.
Таблица 6. Влияние модели турбулентности
Расчёты показали, что результаты полученные с SST моделью более точно согласуются с экспериментальными данным (Сх=0,287)
Сравнение с экспериментом
Сравнение с экспериментом Ахмеда
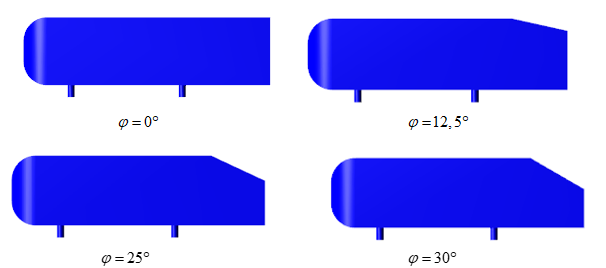
Исследовалось влияние угла скоса φ на величину аэродинамического сопротивления.
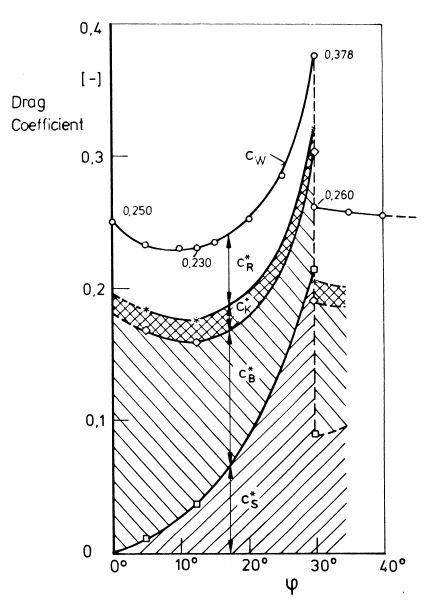
Рис. 10. Результаты эксперимента Ахмеда
Для обтекания тела Ахмеда характерно два критических угла скоса (φ), при которых происходит смена структуры течения.
При φ < 12.5º (первый критический угол) поток отрывается от поверхности тела только вблизи задней кромки. В циркуляционной зоне возникают встречно вращающиеся вихри, образованные потоками со скошенной и боковой поверхностей.
При 12.5º ≤ φ < 30º значительное влияние на параметры потока оказывают трёхмерные эффекты перетекания потоков - усиливается вихреобразование в зоне донного следа.
При φ ≥ 30º поток отрывается на скошенной поверхности тела. На момент отрыва потока влияет величина числа Рейнольдса (Re). В эксперименте Ахмеда исследовалось изменение структуры течения как при низких, так и при высоких числах Re.
Рис. 11. Расчётные модели
Результаты расчёта во FlowVision в целом удовлетворительно соотносятся с экспериментальными данными (но могло быть и лучше!). Максимальное рассогласование составляет 12% и наблюдается в районе первого критического угла.
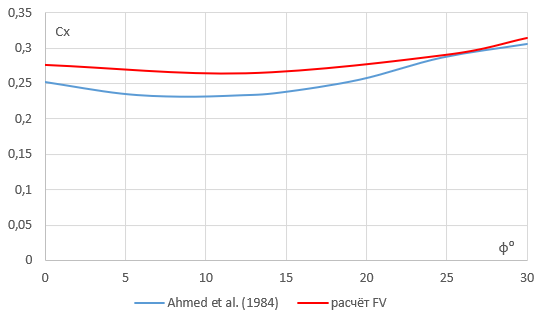Рис. 12. Сравнительный анализ расчёта во FlowVision и эксперимента Ахмеда
Сравнение с экспериментом при изменении скорости
В рамках верификационного исследования было проведено ещё одно сравнение – на этот раз с экспериментом по изменению скорости набегающего потока.
Три расчётные точки определялись для скоростей набегающего потока: V = 10, 30, 60 м/с.
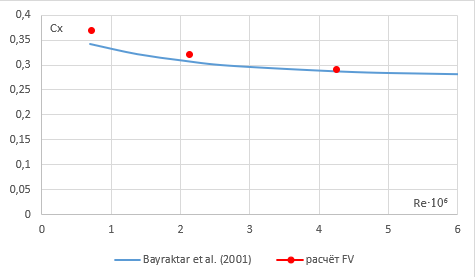Рис. 13. Сравнительный анализ расчёта во FlowVision и эксперимента
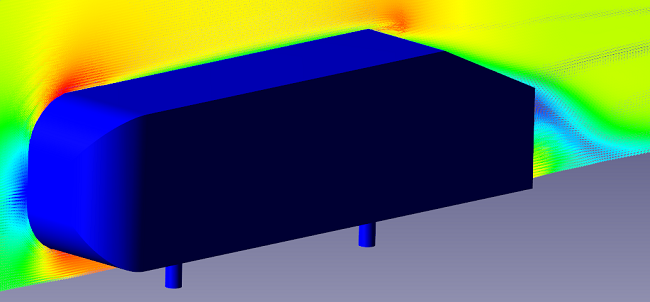
Визуализация течения
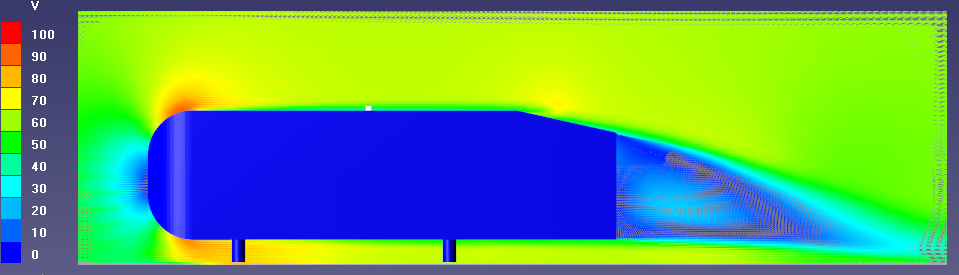φ = 12.5º : обширная застойная зона, вихреобразование умеренное
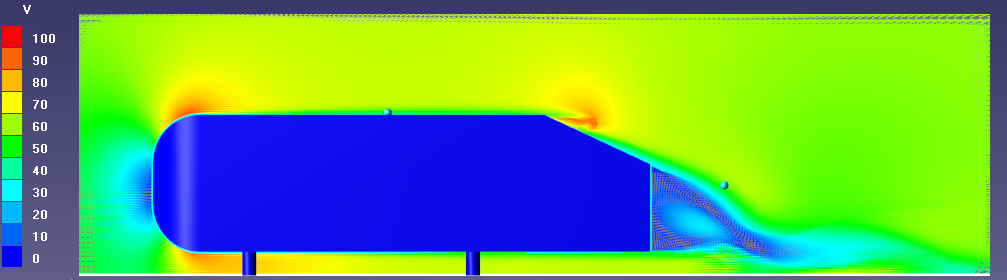φ = 25º : формирование вихрей в донном следе
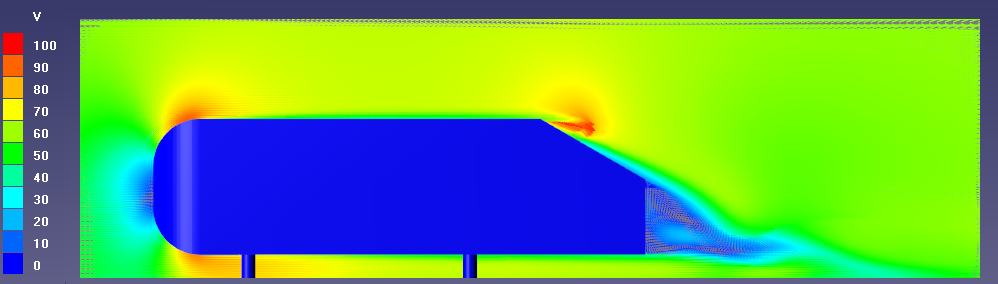φ = 30º : отрыв потока на скошенной поверхности тела
Выводы
Погрешность расчёта большая - 12%, могло бы быть лучше! Но задача считалась на весьма грубой сетке, которая не соответствует желаемому y+=39, найденному в результате исследования сходимости.
В следующей статье мы рассмотрим, можно ли получить более точные результаты и понадобится для этого кластер или нет.
h title="Читайте в следующей статье" alt="Читайте в следую" class="system-pagebreak" /> <h3>Чи"айте далее
В следующей статье мы хотим ответить на вопросы:
- Достаточно ли подробно учитывается вихреобразование в области следа?
- Каковы пределы в стремлении сэкономить в количестве ячеек расчётной сетки?
- Будем ли мы применять LES модель к решению?
- Потребуется ли для данного расчёта кластер?
Все статьи из цикла: