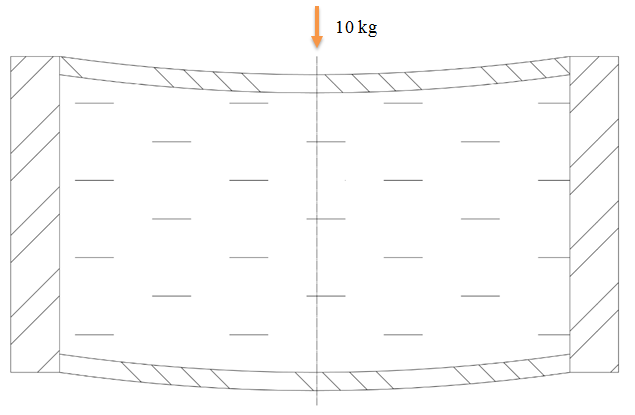
В предыдущем уроке была рассмотрена задача о гидравлическом демпфере с применением технологии «вывернутого» подвижного тела. Запуск этой задачи на расчёт - не тривиальная задача, требующая нестандартного подхода. Для получения стабильного решения зададим коэффициенты искусственной сжимаемости.
В ходе решения данной задачи, внешние стенки расчётной области менялись асинхронно. То есть на первом шаге прикладывается нагрузка на верхнюю стенку, и происходит деформация в Abaqus. Деформация нижней стенки должна будет осуществляться на следующей итерации под действием нагрузок из FlowVision, вызванных изменением давления. Этот алгоритм описывает особенности использования разделённого подхода к осуществлению совместного расчёта.
Совместный расчёт между Abaqus и FlowVision – вид анализа, позволяющий оценить взаимодействие движущегося или деформируемого тела с внутренним или внешним потоком.
Совместный расчет может быть реализован следующими подходами:
• Монолитный подход: уравнения гидро- аэродинамики и прочности решаются одним солвером.
• Разделённый подход: для расчёта задействовано два солвера, каждый из которых решает определённые уравнения. Данный метод реализован в связке FlowVision-Abaqus.
В монолитном подходе взаимодействие жидкости и структуры на взаимной границе рассматривается синхронно, что позволяет сохранить энергию в системе. Это приводит к усилению численной стабильности решения. Но такой подход направлен на решение одной определенной задачи. Решение задачи с новыми начальными условиями или совершенной иной задачи требуют доработки солвера, а также дополнительных исследований.
Именно поэтому большинство задач требует использования специализированных решателей. Например, прочностой решатель считает только прочность оболочек, а гидродинамический - внутренний поток в этой оболочке. Взаимодействие решателей реализуется с помощью разделённого подхода. В разделённой схеме уравнения жидкости и структуры попеременно интегрируются по времени, а условия взаимодействия асинхронны. Это приводит к увеличению энергии в системе, и формированию нестабильности решения. Парирование численной нестабильности реализуется либо за счёт уменьшения шага по времени, либо путём введения демпфирующих коэффициентов.