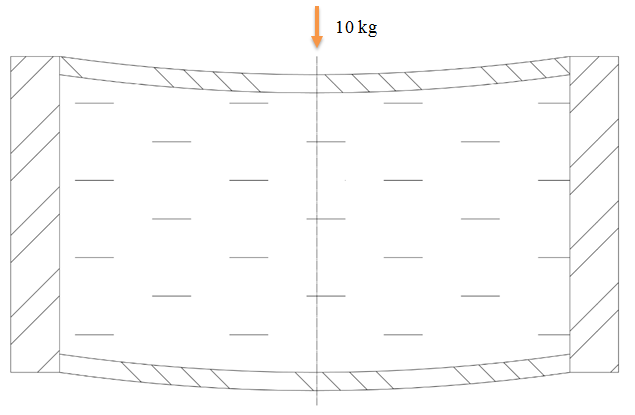
В предыдущем уроке была рассмотрена задача о гидравлическом демпфере с применением технологии «вывернутого» подвижного тела. Запуск этой задачи на расчёт - не тривиальная задача, требующая нестандартного подхода. Для получения стабильного решения зададим коэффициенты искусственной сжимаемости.
В ходе решения данной задачи, внешние стенки расчётной области менялись асинхронно. То есть на первом шаге прикладывается нагрузка на верхнюю стенку, и происходит деформация в Abaqus. Деформация нижней стенки должна будет осуществляться на следующей итерации под действием нагрузок из FlowVision, вызванных изменением давления. Этот алгоритм описывает особенности использования разделённого подхода к осуществлению совместного расчёта.
Совместный расчёт между Abaqus и FlowVision – вид анализа, позволяющий оценить взаимодействие движущегося или деформируемого тела с внутренним или внешним потоком.
Совместный расчет может быть реализован следующими подходами:
• Монолитный подход: уравнения гидро- аэродинамики и прочности решаются одним солвером.
• Разделённый подход: для расчёта задействовано два солвера, каждый из которых решает определённые уравнения. Данный метод реализован в связке FlowVision-Abaqus.
В монолитном подходе взаимодействие жидкости и структуры на взаимной границе рассматривается синхронно, что позволяет сохранить энергию в системе. Это приводит к усилению численной стабильности решения. Но такой подход направлен на решение одной определенной задачи. Решение задачи с новыми начальными условиями или совершенной иной задачи требуют доработки солвера, а также дополнительных исследований.
Именно поэтому большинство задач требует использования специализированных решателей. Например, прочностой решатель считает только прочность оболочек, а гидродинамический - внутренний поток в этой оболочке. Взаимодействие решателей реализуется с помощью разделённого подхода. В разделённой схеме уравнения жидкости и структуры попеременно интегрируются по времени, а условия взаимодействия асинхронны. Это приводит к увеличению энергии в системе, и формированию нестабильности решения. Парирование численной нестабильности реализуется либо за счёт уменьшения шага по времени, либо путём введения демпфирующих коэффициентов.
Составляющие искусственной сжимаемости
Искусственная сжимаемость вводится для уменьшения нестабильности возле деформируемых стенок в CFD-коде. Она задаётся как сопротивление резкому изменению давления.
Искусственная сжимаемость формируется на основе двух коэффициентов:
• Податливость
• Мобильность
Оба коэффициента могут быть использованы как вместе, так и по отдельности.
Скорость стенки на следующем шаге определяется соотношением: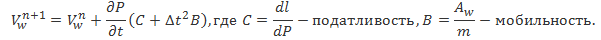
Уравнение показывает, что нестабильность решения происходит за счёт резкого изменения скорости стенки, которая также используется для решения уравнений Навье-Стокса.
Податливость материала (обратно жесткости материала в прочности) характеризуется способностью конструкции (стенки) перемещаться под давлением, приложенным к этой конструкции (стенке). Использование данного параметра целесообразно при незначительном изменении шага по времени в процессе расчёта. В таком случае, однажды заданный коэффициент будет стабильно работать во время расчёта.
Мобильность материала характеризует ускорение стенки под действием приложенного давления и имеет сильную зависимость от изменения шага по времени. Данный коэффициент эффективно использовать при сильном изменении шага по времени (в более чем 10 раз).
Формулы, по которым вычисляются данные коэффициенты, являются начальной оценкой искусственной сжимаемости. Эта оценка может быть избыточной (приводить к значительному изменению веса или сильному демпфированию) или неадекватной. В этом случае, требуется проведение дополнительной оценки путем изменения коэффициентов.
Предлагаю Вам ознакомиться с процессом поиска коэффициентов искусственной сжимаемости на примере задачи о гидравлическом демпфере.
Поиск коэффициентов искусственной сжимаемости
Расчёт податливости в Abaqus
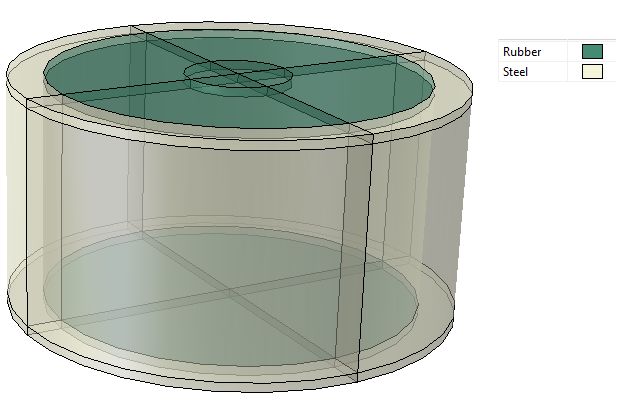
Модель представляет из себя цилиндр с заданной толщиной стенки для определенного материала. Самым податливым материалом в данной модели является гиперэластичный элемент; деформация стали в этой задаче незначительна. Таким образом, необходимо оценивать податливость гиперупругого элемента, как самого деформируемого.
В Abaqus/CAE выберите File>Import>Model и импортируйте CylFSI.inp
Для более точной оценки величины податливости необходимо вычислять изменение нагрузки и смещения под действием данной нагрузки за малый промежуток времени. Рекомендуется при поиске коэффициента использовать небольшой шаг по времени в проекте Abaqus.
Перейдите в модуль Steps и для шага FSI настройте следующие параметры:
• Basic > Time period > 1
• Incrementation:
o Initial increment size: 1E-6
o Maximum increment size: 1E-6
В контекстном меню Loads > Gravity выберите пункт Suppress. Данная нагрузка будет скрыта из анализа.
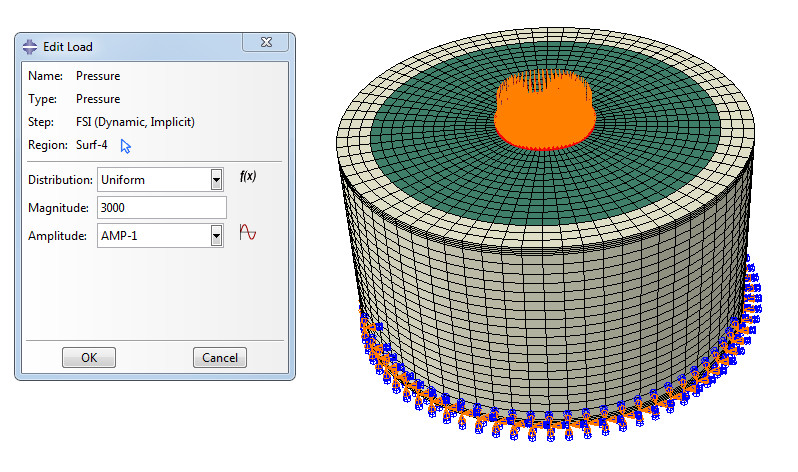
Вместо нее создайте давление и приложите его к поверхности, как показано на рисунке ниже. Значение давления необходимо задать 3000 Па. Также в поле Amplitude необходимо выбрать уже существующее значение амплитуды Amp-1.
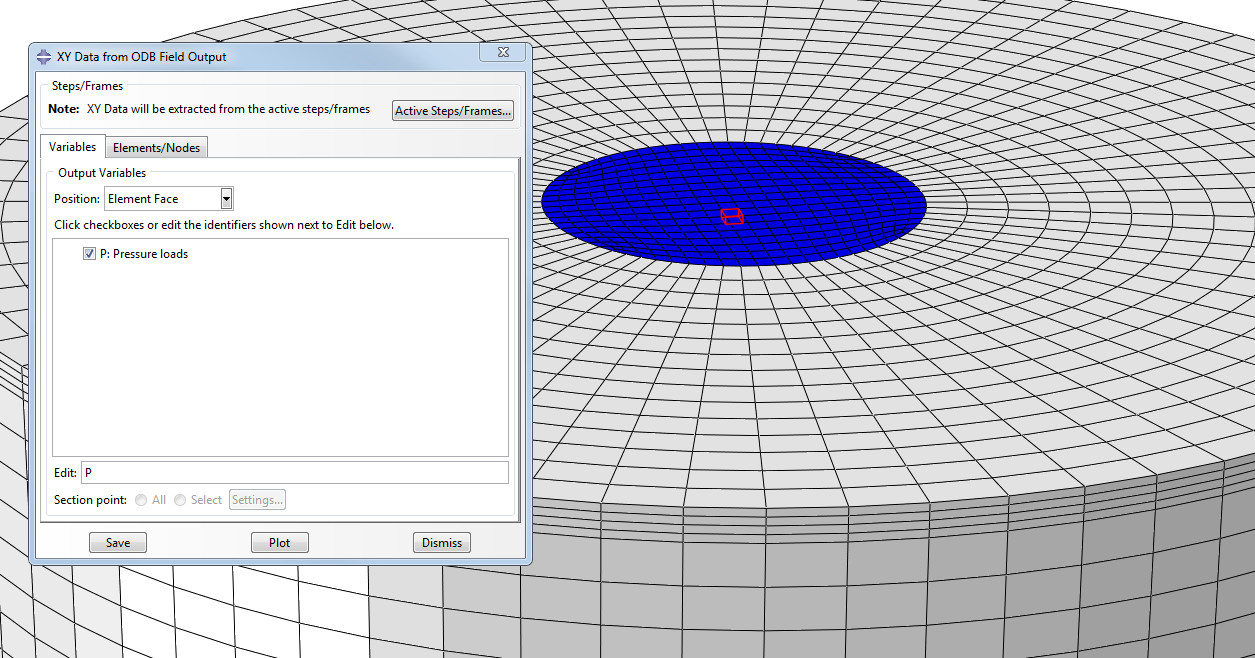
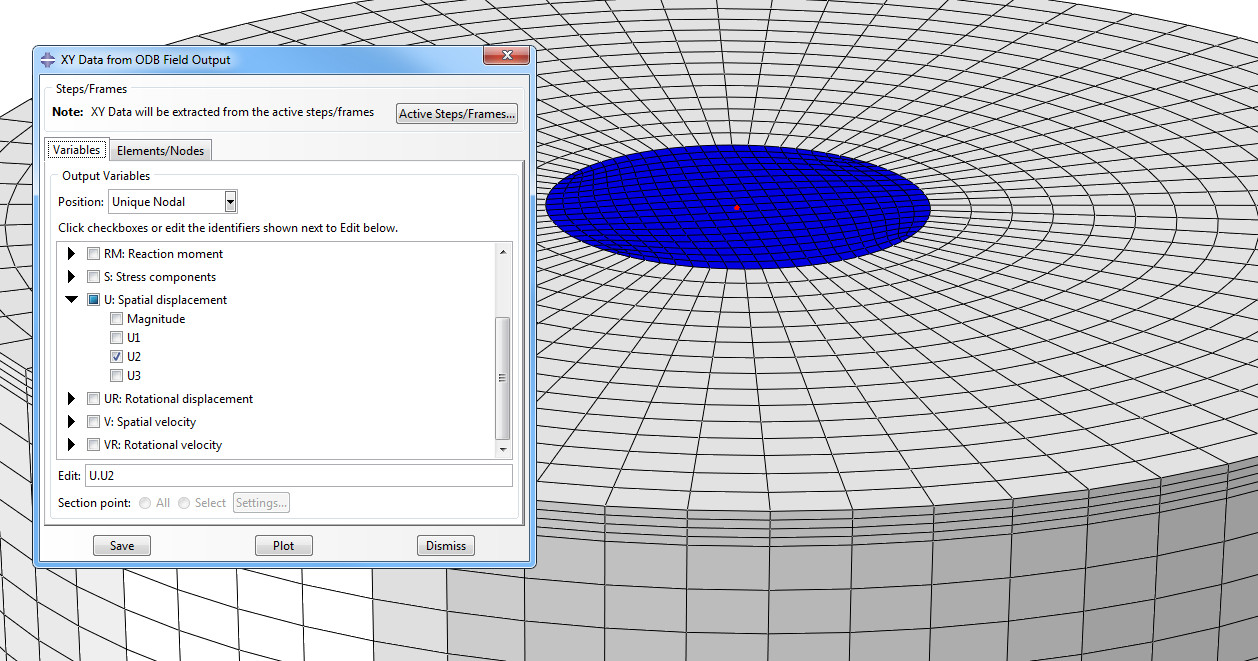
Запустите проект на расчёт. Дождитесь, пока насчитается 30-50 итераций и откройте ODB-файл расчёта. С помощью Create XY Data > ODB Field Output создайте графики давления (переменная P, поверхность элемента – Element Face) и перемещения вдоль оси Y (узел – Unique Nodal).
Графики можно экспортировать в Excel с помощью Plugins > Tools > Excel Utilities...
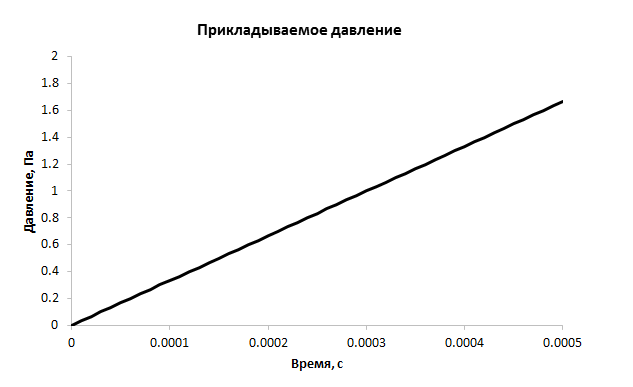
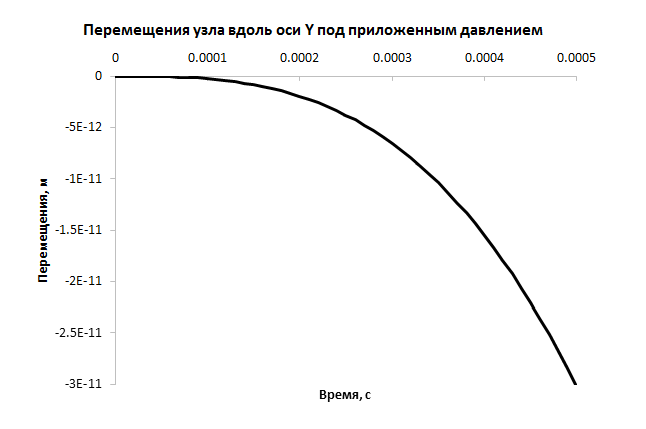
По полученным данным рассчитайте значение податливости как приращение перемещения к приращению нагрузки: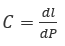 .
.
Рекомендуется искать данное значение с 30-50 итерации, так как в начале расчёта прикладывается несущественная нагрузка.
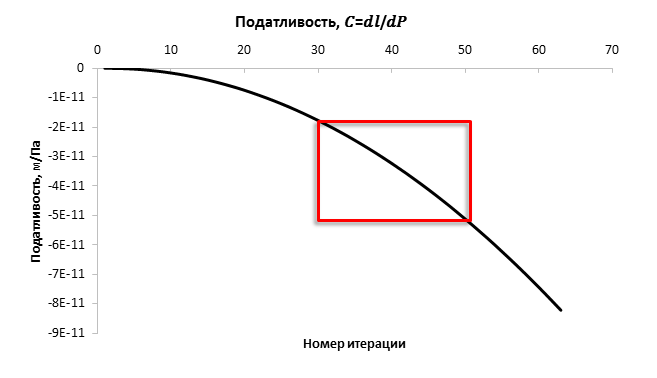
Податливость > C ≈ 5E-11 м/Па
Примечание: Так как вектор перемещения направлен против оси Y, то в этом случае следует брать модуль приращения податливости.
Расчёт мобильности
Для расчёта мобильности необходимо знать площадь поверхности и массу тела, которое будет взаимодействовать с жидкостью.
Массу тела можно найти с помощью Abaqus/CAE. Импортируйте CylFSI.inp.
Для того, чтобы отобразить гиперэластичную часть необходимо перейти в Tools > Display Group > Create… > Item: Sets и выбрать PART-1-1.SET-2. В окне Perform a Boolean on the viewport contents and the selection необходимо нажать Replace и закрыть окно Create Display Group.
В модуле Mesh, с помощью инструмента Tools > Query > Mass Properties, найдите массу гиперэластичных элементов. Значение массы составляет 0.0511 кг.
Площадь поверхности можно найти с помощью FlowVision. Файл > Настройки > Отображение > Показать все группы выберите Да и нажмите Ок. Для объекта Регион > Подобласти > Конус/цилидр #0-сетка> Геометрия > Подвижное тело #0 выберите группу, соответствующую поверхности гиперэластичного элемента, и в окне свойств данной группы будет отображена площадь её поверхности. Площадь поверхности данной группы составляет 0.0055 м2. Площадь гиперэластичных элементов - 0.011 м2.
Значение мобильности вычисляется как 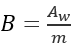 .
.
Мобильность > B = 0.21 м2/кг.
Исследование влияния искусственной сжимаемости
Полученные значения необходимо задать в поле Регион > Подобласти > Подобласть #0 > Модификаторы > Окно свойств подвижного тела #0:
- Искусственная сжимаемость > Да
- Податливость > 5E-11
- Мобильность > 0.21
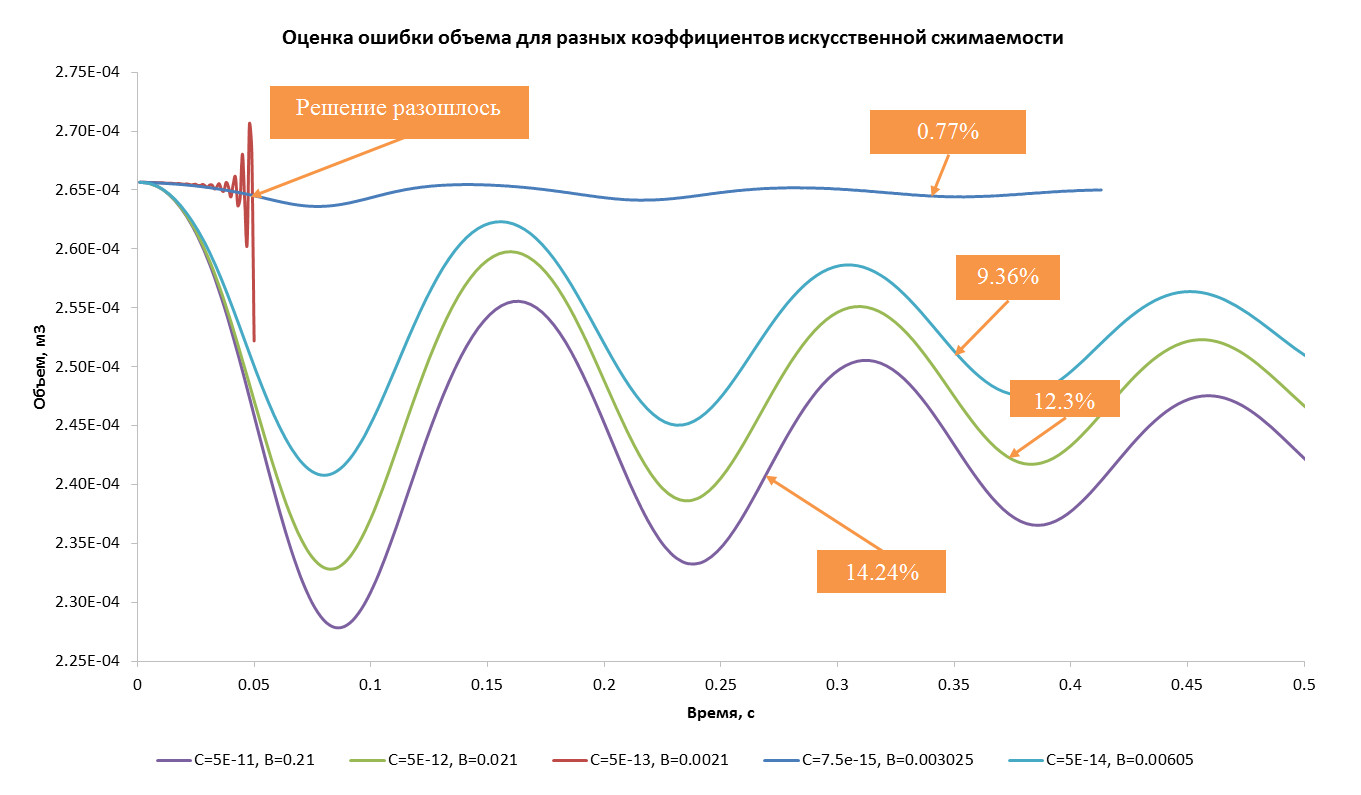
Запустите расчёт и дождитесь, пока объем в системе не начнет сходится. Из полученного графика можно оценить величину ошибки, которую вносит искусственная сжимаемость в расчёт.
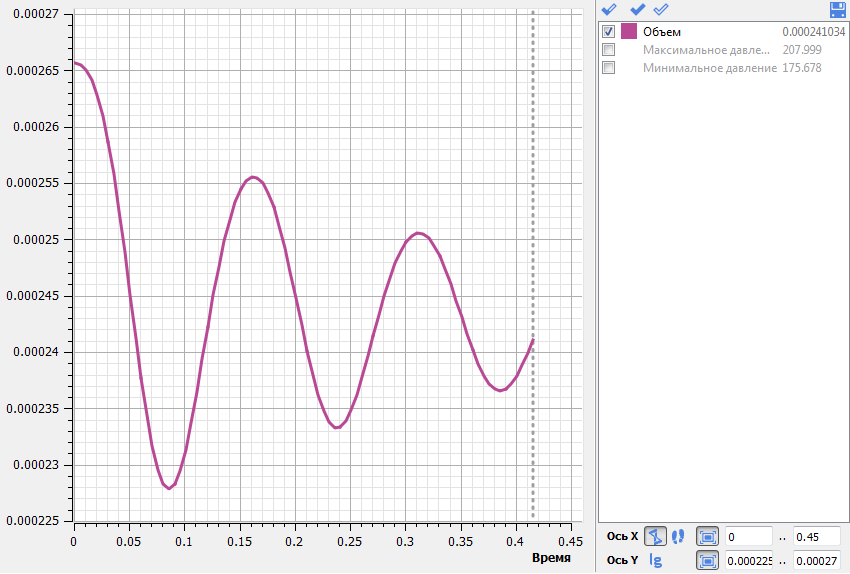
Соответственно, уменьшая коэффициенты искусственной сжимаемости, можно уменьшить ошибку, но также получить развал решения. Для оценки необходимо провести несколько итераций, используя различные коэффициенты искусственной сжимаемости, например, увеличивая или уменьшая на порядок/в разы.
Величину ошибки следует оценивать как 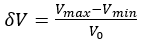 .
.
В итоге, выбираются коэффициенты, при которых ошибка достигает 0.77%:
- Податливость 7E-15 м/Па
- Мобильность 0.003025 м2/кг (значение мобильности было уменьшено в 10 раз)
При использовании этих коэффициентов достигается минимальная ошибка, что позволит получить стабильное и точное решение.
Представленные коэффициенты являются оптимальными: при уменьшении или увеличении их значения наблюдается отрицательное влияние на решение данной задачи.