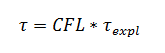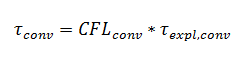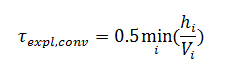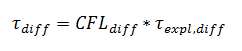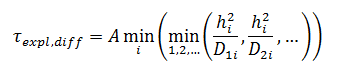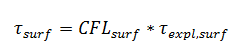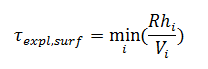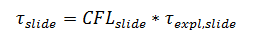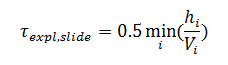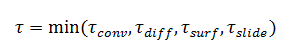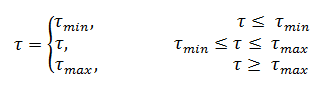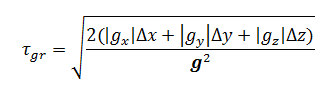Чтобы решить численную задачу, необходимо дискретизировать пространство и время. Вводится шкала времени, позволяющая на основе начальных и граничных условий отыскать промежуточные решения. Постепенно продираясь через промежуточные решения, получаем финальное, которое можно будет использовать для достижения поставленных целей: выбор правильной краски для обшивки ракеты, вычисление скорости вытекания вашего любимого кетчупа или получение оптимальной температуры мойки кота.
Интервалы, через которые программа ищет решение, обычно называются шагом по времени (Time step). Он может быть постоянным или вычисляться для каждой итерации на основе определенных критериев. Следует обратить внимание, что для каждой конкретной программы и задачи шаг по времени разный.
Как же его правильно задать - расскажем в этой статье.
- Что такое шаг по времени во FlowVision;
- Как его выбрать для определенной задачи;
- Как он считается;
- Некоторые полезные приёмы.
Шаг по времени во FlowVision
FlowVision позволяет выбрать шаг по времени:
- Постоянный – решение ДУ будет определяться через одинаковые интервалы времени на протяжении всего расчёта;
- С помощью CFL – используется Критерий Куранта — Фридрихса — Леви — Википедия (критерий КФЛ/CFL), который контролирует шаг по времени на основе текущих расчётных характеристик.
Постоянный шаг
С постоянным шагом по времени всё не так интересно – разбил временную шкалу нужным интервалом (обычно менее 0,1 от характерного времени) и ждёшь пока либо решение сойдется, либо закончится заданное время расчёта.
Самые распостраненные задачи, которые решаются с постоянным шагом по времени:
- Внутреннее течение в трубе. Характерное время - пролётное;
- Внешнее обтекание тела. Характерное время - отношение размера тела к скорости набегающего потока;
- Замкнутое течение. Характерное время - то, за которое частица потока совершает оборот в расчетной области.
Число CFL
С критерием CFL немного сложнее. Сам критерий – это необходимое условие устойчивости явного численного решения некоторых диффуров в частных производных. То есть шаг по времени должен быть меньше определённого значения, иначе результаты моделирования будут нефизичны.
Расшифруем определение с википедии: FlowVision сам считает шаг по времени, с которым ему будет комфортно вести расчёт на основе уже полученного решения. А пользователь лишь масштабирует это значение.
Шаг, который FlowVision считает сам, называется явным шагом по времени (τexpl). Коэффициент масштабирования - число CFL. Итоговый шаг по времени (τ) вычисляется по формуле:
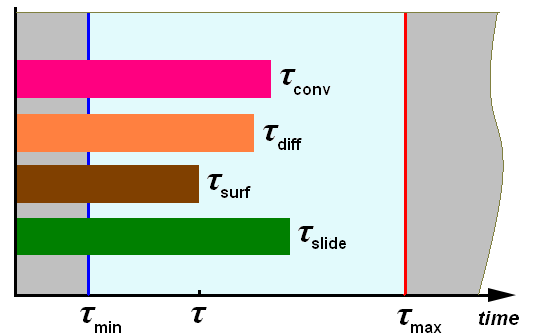
Открыв вкладку Солвер > Шаг по времени, можно увидеть, что критериев то целых четыре штуки:
- Конвективное CFL;
- Поверхностное CFL;
- Диффузионное CFL;
- CFL для скользящей поверхности.
Каждому критерию соответствует свой явный шаг, который вычисляет FlowVision:
- Конвективный явный шаг τexpl,conv;
- Поверхностный явный шаг τexpl,surf;
- Диффузионный явный шаг τexpl,diff;
- Явный шаг для скользящей поверхностей τexpl,slide;
Ограничителем для вышеперечисленных шагов по времени является
- Гравитационный шаг τgr .
Возможно, у вас уже возникло много вопросов:
- Почему критериев и явных шагов так много?
- Как вычисляется тогда шаг по времени, раз критериев и явных шагов так много?
- Зачем нужен гравитационный шаг? И почему у него нет критерия?
Давайте отвечать на каждый вопрос по порядку.
Почему критериев и явных шагов так много?
FlowVision позволяет моделирует разные процессы, для которых необходимо решать разные уравнения: движения жидкости, многофазного взаимодействия, теплопереноса, массопереноса и многие другие. В зависимости от решаемой задачи, выбирается тот или иной критерий расчёта шага по времени.
Рассмотрим движение лодки по волнам. В процессе решения такой задачи моделируется:
- Движение жидкости;
- Движение лодки;
- Движение свободной поверхности - границы раздела фаз: вода - воздух.
Диффузия и скользящая поверхность отсутствуют, а значит нет и смысла рассматривать эти критерии для вычисления итогового шага по времени этой конкретной задачи. Остаются конвективный и поверхностный критерии.
При моделировании движения тел, необходимо задавать поверхностный CFL = 1.
Или другой пример: задача массопереноса частиц. В процессе решения задачи моделируется:
- Движение фазы;
- Движение дисперсных частиц.
Скользящей поверхности все ещё нет, так же нет подвижных тел и движения свободной поверхности. Поэтому будут использоваться только конвективный и диффузионный критерии.
Для задачи с вращением при наличии скользящих поверхностей, необходимо задавать скользящий CFL = 1
Если физический процесс, задающий критерий, не рассматривается в вашей задаче, то критерию (числу CFL) необходимо присвоить значение 1e+20. В такой постановке критерий не будет учитываться.
Рассмотрим каждый критерий и его явный шаг по отдельности.
Конвективный CFL
Используется для большинства задач, где присутствует движение.
Общая рекомендация по выбору значения для данного критерия - выполнение исследования сходимости по шагу.
Все задачи разные и требуют своего определенного шага по времени. Поэтому необходимо исследовать зависимость характерной контрольной величины от шага по времени.
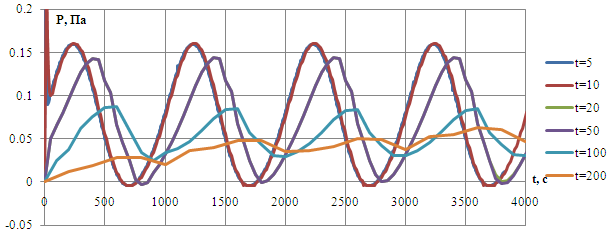
Например, исследуя перепад давления в трубе с переменной скоростью на входе, можно отметить как при различных шагах меняется и величина перепад давления. При определённой величине шага по времени (t < 20), значения контрольной величины не изменяются - это и есть искомый шаг по времени.
Рассчитывается шаг по времени следующим образом:
Конвективный CFL масштабирует явный конвективный шаг по времени, который рассчитывается как:
Для расчёта явного шага по времени FlowVision определяет в пределах всей подобласти минимальное отношение размера ячейки к скорости в этой ячейки. Прикинув размер ячейки и оценив скорость для конкретной задачи, можно и самому оценить по формуле какой шаг будет в объеме.
Для сверхзвуковых течений рекомендуется использовать конвективный CFL 1…10, для дозвуковых можно начать и с больших значений 30…100 CFL.
Диффузионный CFL
Используется для вычисления диффузионного шага по времени:
То есть диффузионный CFL так же масштабирует явный диффузионный шаг по времени:
Где A = 1 задаётся для неявной схемы и A = 0.25 - для явной схемы, обеспечивая ей устойчивость.
Диффузионный явный шаг рассчитывается как минимальное время, за которое возмущение скорости диффузионно распространяется в пределах ячейки. Этот шаг используют для моделирования вязких течений, химических реакций и при использовании анизотропии.
При моделировании задавайте от 10 до 1000 Диффузионных CFL.
Поверхностный CFL
Используется в любых задачах, где моделируется движение свободной поверхности или подвижных тел. Данный критерий ограничивает шаг так, чтобы тело или поверхность не смогли пересечь более чем одну ячейку за одну итерацию. Если тело будет пересекать более одной ячейки за раз, то расчет получится далеко не физичным.
Величина шага для таких задач соответствующая: поверхностный CFL= 1.
Рассчитывается поверхностный шаг как:
Где явный шаг рассчитывается FlowVision как минимум отношения размера ячейки, содержащей свободную поверхность или подвижное тело, к модулю скорости в на границе фазы/подвижного тела:
R – коэффициент, увеличивающий устойчивость расчета. Для свободной поверхности R = 0.5, а для подвижного тела R = 1.
Скользящий CFL
Позволяет вычислить шаг по времени для скользящей поверхности:
Явный шаг вычисляется как минимальное отношение размера ячеек на скользящей поверхности к линейной скорости на этой скользящей поверхности.
Задается строго равный 1.
В случае использования «замороженного ротора» - не учитывается в расчёте шага по времени.
Как вычисляется тогда шаг по времени, раз критериев и явных шагов так много?
Сам шаг по времени вычисляется исходя из минимального значения от шагов по времени, полученных с помощью всех заданных критериев:
Помимо того, что выбирается минимальное значение, также учитываются ограничители шага, шаг сравнивается с минимальным и максимальным шагами по времени, которые задаются пользователем:
Зачем нужен гравитационный шаг? И почему у него нет критерия?
Гравитационный шаг вводится для проектов, где задан вектор гравитации. Наличие гравитации может существенно как ускорить тело, так и замедлить его. Это может соответственно увеличить или уменьшить шаг по времени. Чтобы ограничить поверхностный и конвективный явные шаги сверху, считается гравитационный шаг.
Он вычисляется как:
Где:
- g - вектор гравитации;
- gi - компоненты вектора гравитации;
- Δi - минимальные размеры ячеек.
Лайфхаки
- При решении задачи необходимо понимать, какая физика сейчас влияет на решение и периодически сверяться с характерным шагом для данной задачи.
- Если шаг по времени проседает (то есть резко уменьшается) относительно ожидаемого, необходимо задуматься, всё ли задано корректно и правильно считается. Самой простой диагностикой является вывод «Внутренних характеристик» в окно мониторинга, таких как:
- Шаг по времени;
- Явный шаг по времени (считается как явный конвективный шаг).
Для облегчения поиска области, из-за которой шаг проседает, во FlowVision можно отображать данные величины как в объеме, так и на плоскости.
- Возможно ли такое, чтобы шаг по времени становился меньше, чем явный шаг по времени?
Да, такое возможно, так как во FlowVision шаг по времени считается два раза за итерацию. В начале итерации считается шаг по времени на основе всех шагов. После этого происходит вставка подвижного тела и идет пересчёт явного конвективного шага. Новый шаг по времени уже не вычисляется! Поэтому вполне возможен случай, что новый явный шаг по времени будет больше, чем шаг по времени.