При решении задач гидродинамики численными методами неизбежно приходится сталкиваться с неудовлетворительной точностью получаемых результатов. Причин этому может быть очень много. Но одной из наиболее распространенных является недостаточное разрешение расчетной сеткой.
Процесс поиска минимально необходимой расчетной сетки для получения качественного расчета в задаче (или классе задач) называется исследованием сходимости по расчетной сетке.
В данной статье рассмотрены такие вопросы, как:
- Что такое сеточная сходимость и почему её необходимо достигать
- Как лучше всего проводить исследование сходимости по сетке
- Что бывает, когда исследованием по сетке пренебрегают или не доводят до победного конца
- Что делать если сходимость нельзя достигнуть из-за недостатка вычислительных ресурсов, но результат получить очень хочется
Что такое сходимость по сетке? Почему без нее нельзя?
В основе метода конечных объемов, применяемого во FlowVision, лежит аппроксимация расчетного пространства конечными объемами – расчетными ячейками. Весь расчетный объем разбивается на параллелепипеды и многогранные ячейки у граничных условий. Затем производится вычисление потоков физических величин входящих и исходящих через каждую грань ячейки.
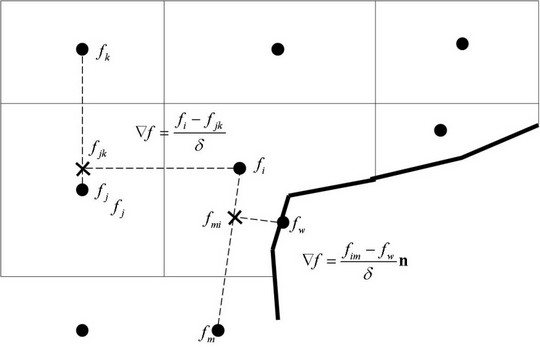
Рис. 1. Аппроксимация градиента переменной на гранях приграничной ячейки.
Чем мельче размер конечных объемов (расчетных ячеек) относительно размеров всего расчетного объема, тем выше разрешение расчетного объема. Здесь можно провести прямую аналогию с разрешением монитора компьютера: выше разрешение – больше детализация.
При моделировании физических процессов всегда необходимо представлять, какая особенность процесса является определяющей, ключевой для поставленной задачи, имеет наибольшее влияние на результат. Именно эта особенность (деталь конструкции, вихрь, источник тепла, профиль скорости у стенки) должна быть разрешена расчетной сеткой в первую очередь.
Например, при моделировании обтекания самолета вполне допустимо пренебречь геометрией заклепок. Разрешать расчетной сеткой каждую заклепку нецелесообразно, т.к. возмущение потока, порожденное заклепкой несущественно по сравнению с теми градиентами давления, которые создает, например, закрылок.
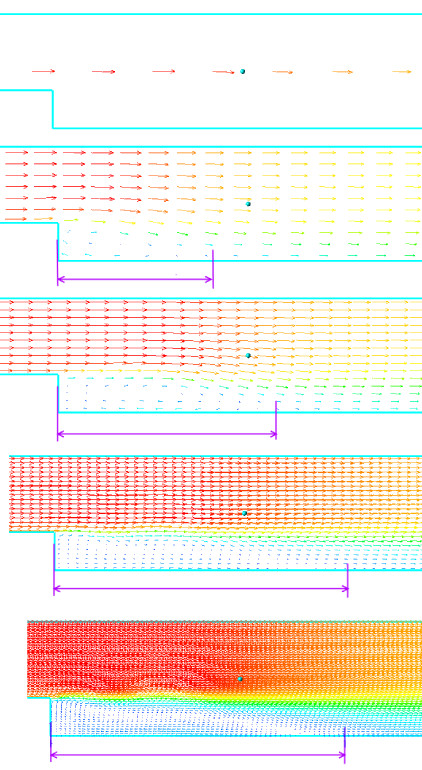
На рисунке 2 видно, первая картинка представляет собой предельный случай – только одна ячейка на высоту канала не позволяет наблюдать никаких вихрей. При грубой сетке вихрь наблюдается, но за обратным уступом существенно короче, чем при сетке высокого разрешения. Связано это с тем, что вихрь плохо разрешен по высоте и быстро прижимается основным потоком, не успев развиться в протяженную теневую зону за уступом.
Рис. 2. Картина течения за обратным уступом при различном разрешении расчетной сетки. Сверху-вниз: разрешение от 1 ячейки по высоте до 240 по высоте.
Однако даже если хорошо себе представлять, какая особенность моделируемого физического процесса нуждается в хорошем пространственном разрешении, не всегда возможно однозначно сказать, какого разрешения будет достаточно. По этой причине при решении задач численным методом необходимо выполнять исследование сходимости по сетке.
Подходы к исследованию сходимости по сетке
В общем случае исследование сходимости по сетке заключается в изучении зависимости решения от разрешения пространства с помощью расчетной сетки.
Этапы исследования сходимости по сетке:
- Выбор математической модели: на этом этапе необходимо правильно выбрать набор решаемых уравнений, полностью описывающих ключевые физические процессы, происходящие в моделируемом устройстве.
- Выбор контрольных (характерных) параметров: здесь необходимо определить, какие параметры устройства или течения являются ключевыми, отражают корректность получаемого решения. Эти же параметры, как правило, служат и для определения момента сходимости стационарного решения. Например, для задачи течения по каналам наиболее характерной величиной может являться перепад давления или расход, в случае теплообмена сюда добавляется температура. Для внешнего обтекания тела наибольший интерес могут представлять подъемная сила и сила сопротивления.
- Упрощение расчетной задачи: очень часто исследование сходимости по сетке можно провести на неполной постановке задачи. Взять лишь часть моделируемого устройства с наиболее важным физическим процессом. Например, в случае течения в канале или обтекания трехмерного крыла целесообразно перейти к двухмерной постановке. Сетка, найденная для двумерного случая, почти наверняка подойдет для трехмерного случая. При необходимости можно будет проверить это, проведя расчет в трехмерной постановке на двух сетках. Применение упрощенных постановок задач позволяет на порядки сократить затраты времени и вычислительных ресурсов на этапе исследования сходимости по сетке.
- Выбор начальной расчетной сетки: исследование сходимости можно проводить разными способами, измельчая начальную сетку или применяя адаптацию. В случае адаптации необходимо помнить, что применение высоких уровней адаптации приводит к ухудшению масштабируемости задачи на несколько процессоров. Не используйте уровень адаптации выше 5. С какого размера ячеек стоит начать? Можно отталкиваться от следующих рекомендаций: а) на характерные размеры в задаче (диаметр отверстия, высота уступа, ширина канала или диаметр вихря) должно приходиться минимум 4 ячейки, а лучше 8-10; б) при решении большинства задач внешнего обтекания стартовать стоит с Y+ не больше 1000 - 10 000; в) при отказе от пристеночных функций, т.е. при разрешении пристеночного слоя расчетной сеткой начинать необходимо максимум с Y+ = 1..2.
- Моделирование с последовательным измельчением расчетной сетки: можно выбрать разные стратегии, в зависимости от сложности задачи:
- Для измельчения расчетной сетки применять адаптацию по поверхности и в объеме. Такой подход позволяет использовать ранее посчитанное решение как хорошее начальное приближение для расчета на новой сетке. Второй плюс – экономное измельчение сетки – сетка мельчится только в наиболее интересных инженеру местах.
- Измельчение сетки выполнять перенастраивая начальную сетку. У этого подхода два минуса: размерность задачи будет больше, т.к. фактически адаптируется весь расчетный объем, а не отдельные зоны; расчет каждый раз необходимо запускать с нуля. Данный подход чаще всего применяется в случае двумерных расчетов, когда время счета занимает считанные минуты или часы. Главным преимуществом такого подхода является то, что измельчается именно весь расчетный объем, исключая ошибку инженера, который мог не учесть какой-то характерный процесс за зоной адаптации (за зоной исследования влияния размера ячейки на решение).
- Анализ полученных результатов: после завершения серии расчетов с разным разрешением сетки необходимо построить графики, которые иллюстрируют влияние размера ячейки на характерные величины (определенные на втором шаге). Ось Y на таких графиках – характерная величина; ось X – размер ячейки, либо Y+, либо уровень адаптации. О сеточной сходимости можно говорить тогда, когда наблюдается выход построенного графика на асимптоту, т.е. когда дальнейшее измельчение сетки не приводит к существенному изменению характерных, контролируемых величин.
- Уменьшение расчетной сетки: при исследовании сходимости, особенно в случае измельчения методом перестроения начальной сетки, будет найдена расчетная сетка, которая дает качественный результат, но может не являться оптимальной. Т.е. найденная расчетная сетка может быть избыточной, например, разрешать часть расчетной области, в которой не происходит ничего интересного: нет высоких градиентов физических величин, нет вихрей и геометрических особенностей. Эта часть расчетной области попала в зону высокого разрешения случайно или вследствие недостаточно вдумчивого подхода к построению расчетной сетки. На этом этапе можно редуцировать расчетную сетку в таких «спокойных» местах, каждый раз убеждаясь, что загрубление сетки не приводит к изменению результатов. Другой подход уменьшения числа расчетных ячеек – применение адаптации к решению.
- Модификация сетки с учетом полной постановки задачи: на этом шаге можно проверить, что сетка перенесенная из двухмерной постановки на трехмерную также является оптимальной. Т.е. дальнейшее измельчение ячеек в два раза не приводит к существенному изменению результата. Это всего лишь один расчет и он может уберечь от ошибки. Кроме того, может понадобиться дополнительно разрешить элементы геометрии, которые отсутствовали в двумерной задаче, но могут повлиять на расчет.
Пример исследования сходимости. Шаг за шагом
Решается задача внешнего обтекания трехмерного крыла самолета при числе Маха 0,6.
Шаг 1. Выбор математической модели
Рис.3. Картина течения вокруг крыла конечной длины в трехмерной постановке
При больших числах Маха необходимо учитывать сжимаемость газа, его нагрев. Поэтому кроме уравнений Навье-Стокса необходимо включить расчет уравнения для энергии. Кроме того значение числа Re на несколько порядков больше 1500, поэтому необходимо применять модель турбулентности. В силу трехмерной постановки разрешение пристеночного слоя может оказаться нецелесообразным с точки зрения потребных вычислительных ресурсов. Поэтому выбирается применение пристеночных функций, вместо прямого разрешения пристеночного слоя.
Шаг 2. Выбор контрольных параметров
В данной задаче основными параметрами являются коэффициент сопротивления, коэффициент подъемной силы, коэффициент момента. Причем рассматривать необходимо сразу все три параметра, т.к. сеточная сходимость для каждого из них может быть достигнута при разном разрешении расчетной сетки.
Шаг 3. Упрощение расчетной задачи
Данное крыло имеет конечную длину, но постоянный профиль. Впрочем, даже если бы профиль был не постоянным, все равно, переход к двухмерной постановки является оправданным для экономии ресурсов на этапе исследования сходимости по сетке.
Шаг 4. Выбор начальной сетки
В задачах внешнего обтекания профиля основной интерес лежит в области положения отрыва или скачка (при их наличии), правильное разрешение градиентов давления и корректное определение профиля скорости у стенки, во многом определяющие силу сопротивления. Соответсвенно, во многом надо ориентироваться на Y+. У пристеночной функции есть область применимости: Y+ должен быть больше 3. Это оценка снизу, от нее уже можно отталкиваться. Либо можно отталкиваться от максимального значения Y+ = 10 000. Либо можно стартовать с 10 ячеек по высоте профиля.
Чтобы оценить значение Y+ хотя бы примерно можно провести расчет для сетки с 10 ячейками по высоте профиля и посмотреть на среднее значение Y+. Измельчение такой сетки в два раза будет давать уменьшение Y+ примерно в два раза.
Шаг 5. Моделирование с последовательным измельчением начальной сетки
Как было сказано, основная сеточная интрига в данной задаче заключается в качественном разрешении градиентов у поверхности профиля. По этой причине выбран подход с измельчением поверхности с помощью поверхностной адаптации. Последовательно проведено несколько расчетов, с постепенным увеличением уровня адаптации.
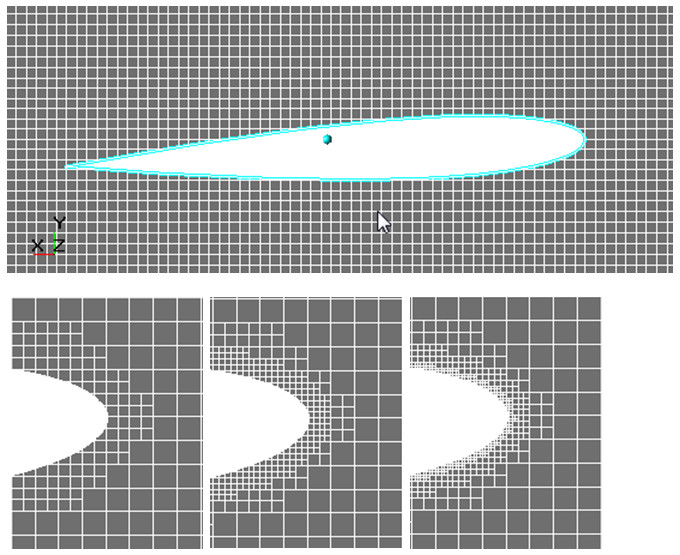
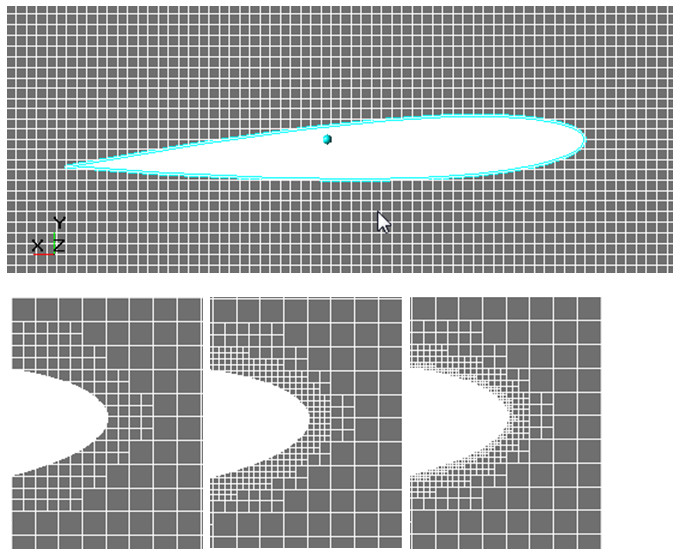
Рис.4. Эволюция расчетной сетки в процессе исследования сходимости по сетке.
Шаг 6. Анализ полученных результатов
В результате исследования была построена следующая диаграмма:
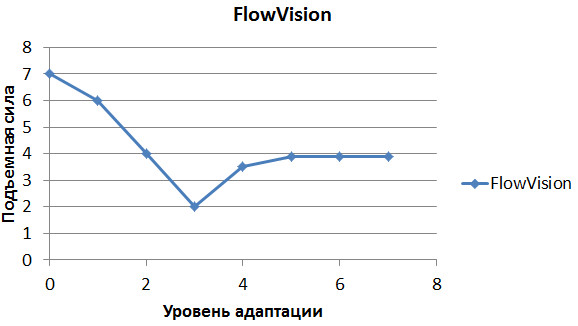
Рис.5 . Зависимость подъемной силы от уровня адаптации по поверхности
Как видно, измельчение сетки после 5ого уровня адаптации влияет на подъемную силу несущественно, можно остановиться на размере ячейки, соответствующем 5ому уровню. Однако если посмотреть на аналогичный график для силы сопротивления, можно заметить, что сходимость по этой силе достигается на более мелких сетках:
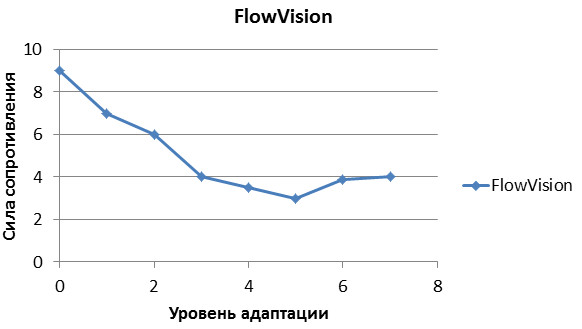
Рис. 6. Зависимость силы сопротивления от уровня адаптации по поверхности
Таким образом необходимо остановить свой выбор на размере ячейки у поверхности , соответствующем шестому уровню адаптации.
Шаг 7. Уменьшение расчетной сетки
В данном исследовании расчетная сетка строилась в несколько слоев на каждый уровень адаптации, чтобы обеспечить плавный переход от одного уровня адаптации к другому, чтобы также аккуратно разрешить градиенты величин, направленные по нормали к поверхности.
Возможно, количество слоев было выбрано избыточное и, если уменьшить количество слоев на каждый уровень адаптации, то можно сэкономить сетку. Для этого запущен расчет с шестым уровнем адаптации и меньшим числом слоев на каждый уровень. Дополнительно, проведен расчет с большим числом слоев, чтобы убедиться, что слоев достаточно:
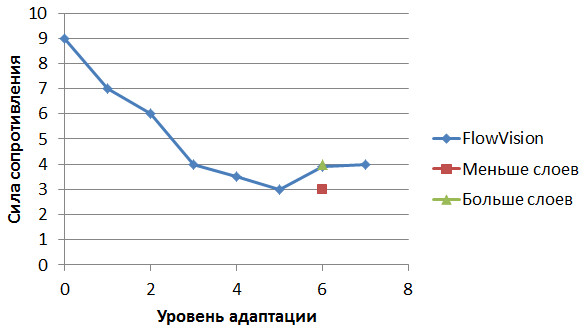
Рис.7 . Исследование влияния числа слоев адаптации на силу сопротивления при шестом уровне адаптации
Как видно, уменьшение числа слоев сказывается негативно на результатах, а увеличение приводит к незначительному изменению. Таким образом уменьшить размерность задачи не представляется возможным - в ходе исследования сходимости была сразу найдена оптимальная расчетная сетка.
Шаг 8. Модификация сетки с учетом полной постановки задачи
При переходе к трехмерной постановке были учтены следующие особенности:
- Необходима объемная адаптация вокруг бокового края крыла, для учета концевых эффектов у крыла конечной длины.
- Применение адаптации высокого уровня (выше четвертого) крайне негативно сказывается на качестве распараллеливания расчета. По этой причине начальная сетка была измельчена в 4 раза, чтобы перейти от шестого уровня адаптации к четвертому. Также дополнительно для улучшения масштабируемости была включена динамическая балансировка сетки.
На что стоит обратить внимание при построении расчетной сетки
- Старайтесь на каждый уровень адаптации использовать минимум 4 слоя, а лучше 8 и более. Плавный переход от сетки разного размера позволяет получить более точное и корректное решение.
- В области ненулевых градиентов физических величин, в области существования вихрей необходимо использовать ячейки, максимально близкие по форме к кубу. Применение вытянутых ячеек в области с непараллельным направлением течения относительно сторон ячеек негативно сказывается на точности и качестве решения.
- Не используйте слишком высокие уровни адаптации, это плохо сказывается на возможностях ускорения расчета с помощью многопроцессорных систем.
- При работе с моделями турбулентности следите за преобладающим значением Y+ . Разные модели турбулентности с и без пристеночных функций имеют ограниченную область применимости.
Что происходит, если не проводить исследование сходимости или не доводить исследование до конца?
Рассмотрим пример, когда пользователь выполняет исследование сходимости, ориентируясь на экспериментальные результаты.
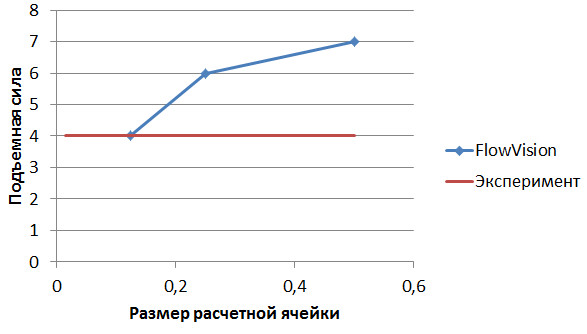
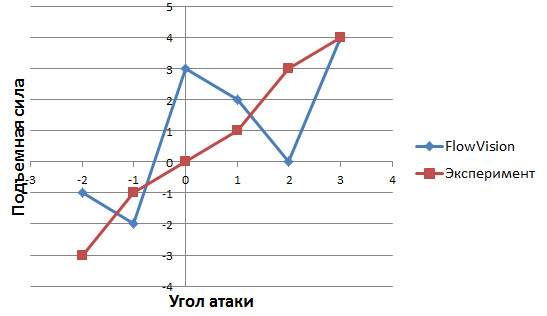
Инженер моделирует обтекание крылового профиля при угле атаки три градуса, пробует измельчать расчетную сетку до тех пор, пока подъемная сила не совпадет с экспериментальными данными (красная линия), см. рис. 8.
Рис.8. Зависимость подъемной силы от размера ячейки. Исследование сходимости, проведенное только до момента пересечения с линией экспериментального значения.
При размере ячейки 0,125 получилось идеальное совпадение с экспериментом. После чего инженер счел, что сходимость по сетке достигнута и возможно приступать к моделированию течения при разных углах атаки. Результат представлен на следующем рисунке:
Рис.9. Зависимость подъемной силы от угла атаки для постановки с недостигнутой сеточной сходимостью.
Как видно, при угле атаки в три градуса мы по-прежнему имеем чудесное совпадение с экспериментом, а вот во всех остальных точках решение может быть даже не соответствующим физике процесса.
Такая ситуация возможна и в тех случаях, когда исследование сходимости по сетке остановлено из-за ограниченных вычислительных ресурсов или времени, а не следствиями из природы численных методов.
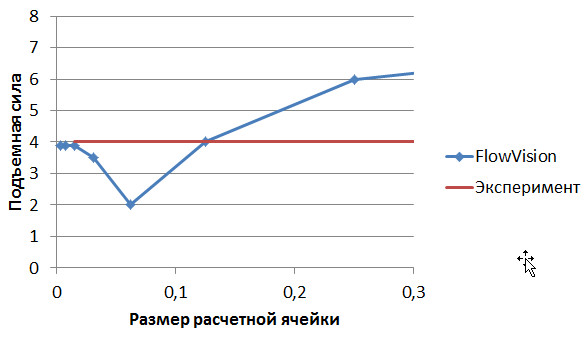
Что было бы, если бы инженер продолжил исследование сходимости по сетке и убедился, что сходимость действительно достигнута?
Рис.10. Зависимость подъемной силы от размера расчетной ячейки. Исследование сходимости по сетке доведено до конца.
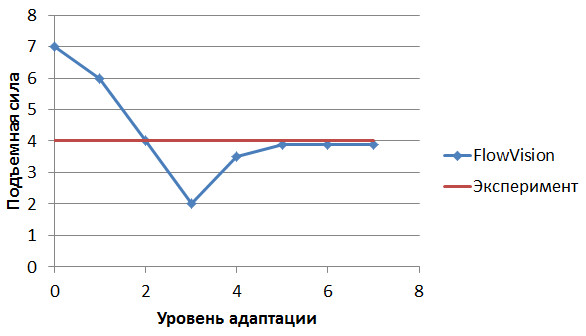
Те же результаты, но построенные не для размера расчетной ячейки, а для уровня адаптации по поверхности профиля:
Рис. 11. Зависимость подъемной силы от уровня адаптации. Исследование сходимости по сетке доведено до конца.
Как видно на рисунке выше, дальнейшее измельчение сетки привело сначала к удалению от экспериментального значения и лишь более высокие уровни адаптации позволили асимптотично подойти к экспериментальному значению.
Почему же решение при размере ячейки в 0,125 м дало такое хорошее совпадение с экспериментом? Ответ очень прост: случайное совпадение. Две кривые имеют очень много шансов когда-нибудь пересечься.
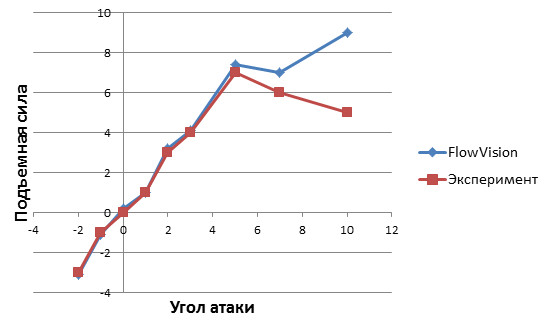
Итак, инженер убедился, что сходимость по сетке на угле атаки в три градуса достигнута. Но результаты моделирования на всем диапазоне углов атаки снова разочаровывают:
Рис.12. Зависимость подъемной силы от угла атаки для расчетной сетки, полученной в ходе корректного исследования сходимости на угле атаки в 3 градуса.
В целом совпадение с экспериментом замечательное, однако, на высоких углах атаки результаты во FlowVision противоречат не только эксперименту, но и знаниям инженера.
Дело в том, что на больших углах атаки сильно меняется физика процесса. Т.е. исследование сходимости по сетке проводилось для малого угла атаки, для безотрывного течения. На большом же угле атаки образовался отрыв, появились вихри, резкие градиенты давления, которые могут быть не разрешены сеткой, идеально подходящей для безотрывного течения.
Таким образом, необходимо учитывать особенности различных режимов работы моделируемого устройства и при необходимости проводить отдельные исследования сходимости. Конечно не для всех режимов, но выделять несколько характерных диапазонов.
Что делать если сходимость нельзя достигнуть из-за недостатка вычислительных ресурсов, но результат получить очень хочется
При моделировании сложных устройств, в которых необходимо учитывать процессы, существенно отличающиеся в геометрических масштабах, сходимость по сетке достигается на десятках, а то и на сотнях миллионов расчетных ячеек. При этом на предприятии просто может не оказаться потребных вычислительных ресурсов. Что делать, если сходимость не достигнута, а оперативной памяти уже не хватает?
Обратимся к истории, когда на заре вычислительной гидродинамики оперативная память ЭВМ исчислялась не терабайтами, а килобайтами. Как удавалось решать сложнейшие задачи?
- Качественный результат важнее количественного: не нужно гнаться за точным совпадением с экспериментом. Главное обеспечить качественно правильное решение, когда на любом режиме течения мы получим ожидаемый результат, а изменение того или иного параметра приведет к изменению решения в ожидаемом направлении. Проверить, что качественно решение правильное можно посчитав устройство на разных режимах течения и убедившись, что кривая эквидистантна экспериментальной или теоретической.
- Двухмерная постановка: переход к двухмерной постановке существенно ускоряет расчет. Оцените, насколько важны те детали, которые удается учесть только в трехмерной постановке. Может от учета их влияния можно отказаться?
- Съешьте слона по частям: проанализируйте стоящую перед Вами задачу. Может быть, большая и сложная задача разбивается на несколько независимых подзадач? А решение каждой такой подзадачи может быть использовано как граничное условие для другой? Простейший пример: сложный трубопровод с клапанами, поворотами и тройниками можно разбить на несколько секций.
Будьте внимательны, попытка удовлетвориться решением без исследования сеточной сходимости может привести к потере времени или более печальным последствиям. Также не забывайте, что в вычислительной гидродинамике есть еще несколько абстракций, влияние которых на решение также необходимо исследовать:
- Граничные условия (их удаленность от объекта исследования, их тип)
- Шаг по времени (разрешаете ли во времени ключевые процессы?)