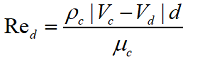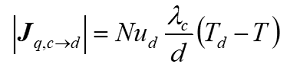Возможности дисперсной фазы: частицы

И пример проекта FlowVision "моделирование течения воды с песком"

Как моделировать частицы?

Если вы задались таким вопросом, знайте - мы и руководство пользователя FlowVision с вами. Но если серьёзно, то вопросы моделирования дисперсной фазы косвенно уже поднимались в статьях о многофазных течениях и обледенении. А нетривиальные примеры горения угля и испарения капель пошагово разобраны в самоучителе.

Но всё же дисперсные задачи неоднозначны и кроют в себе много вопросов. Настало время внести ясность в моделирование частиц! В ходе погружения в дисперсность мы будем останавливаться на ключевых настройках, говорить о текущих возможностях и ограничениях FlowVision и изучать проекты "изнутри". 

Как устроен этот дисперсный цикл?

Следуя контексту дисперсной тематики, предлагаю съесть слона по кусочкам. 

• В этой статье мы поговорим о частицах в общем физическом контексте, рассмотрим подход, реализованный в дисперсном решателе FlowVision, определим классы решаемых задач, обозначим существующие ограничения и вместе промоделируем дисперсное течение (пример: течение воды с песком).
• В следующей статье остановимся на моделировании пузырьков и дроблении капель.
• Заключительная часть будет посвящена моделированию течений в пористых средах.

Также мы не оставим вас без примеров реальных проектов FlowVision. Так определённо будет проще погрузиться в моделирование и отойти от абстрактных понятий. Если возникнут вопросы, не стесняйтесь задавать их команде тех. поддержки через email (support@flowvision.ru).

Начнём с определений

Дисперсная среда – это либо мелкие частицы в газообразном, жидком или твёрдом агрегатном состоянии, либо твёрдое тело, имеющее пустоты (поры). Воспоминания о влажном морском воздухе, песчаном пляже и бокале лимонада не только наводят мысли о приближающемся лете, но и демонстрируют примеры дисперсной среды. В примерах прослеживаются ключевые свойства среды - частицы не существуют сами по себе, а взаимодействуют с несущей их сплошной фазой:

• капельки воды переносятся воздушным потоком
• пузырьки газа всплывают в напитке 
• вода просачивается через грунт

При этом частицы равномерно распределяются между молекулами сплошной фазы, не вступая с ними в химическую реакцию. 

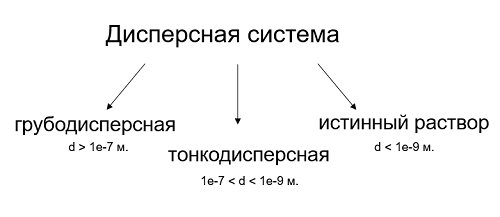
Взаимодействие дисперсной и сплошной фаз формирует дисперсную многофазную систему. В зависимости от размера частиц (d) выделяют грубодисперсные и тонкодисперсные системы. А если диаметр частицы сопоставим с размером молекулы несущей среды, то такая система уже называется истинным раствором. Вовсе не обязательно, чтобы все частицы дисперсной системы обладали одинаковым размером и формой. Скорее наоборот, они будут абсолютно непохожи друг на друга. 

Во FlowVision предполагается, что размер частицы всегда много больше размера молекулы. В начальных и граничных условиях пользователь может задавать как одинаковые частицы (имеющие некоторый средний диаметр), так и спектральные распределения частиц по размерам.

Дисперсность во flowvision: Частицы и Каркас

В зависимости от агрегатного состояния дисперсной и несущей среды образуются разные дисперсные системы. Всё их многообразие представлено на схеме: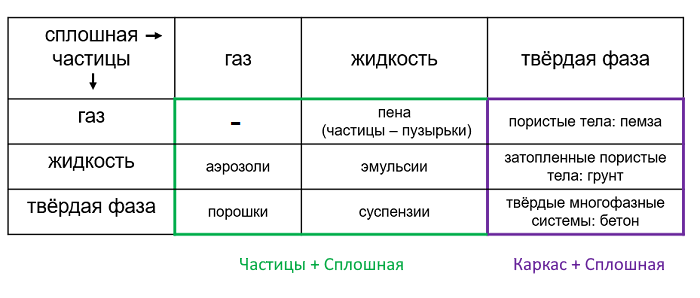Во FlowVision дисперсность в газовой и жидкой среде определяется взаимодействием "Частицы + Сплошная", а твёрдая пористая среда - взаимодействием "Каркас + Сплошная".

Так в чём же разница?

Идеологически фазы "Частицы" и "Каркас" схожи - в рамках Эйлерова подхода каждую из них можно рассматривать как континуум. Однако физика у этих двух фаз разная. Главное отличие в том, что фаза "Каркас" неподвижна. Соответственно, модели и корреляции для частиц и твёрдого неподвижного тела разные: в уравнениях физических процессов для Каркаса отсутствует конвективный член. Да и в целом уравнения Движения и Переноса фазы не актуальны. 

На данном этапе последуем примеру наших разработчиков и разделим повествование о дисперсных возможностях FlowVosion на две ветки: Частицы и Каркас. И далее сконцентрируемся только на Частицах; о применении Каркаса для моделирования теплообменников, фильтров, грунта и других пористых сред мы вернёмся в третьей статье цикла.

Эйлеров подход к моделированию частиц

Во FlowVision при описании частиц их объединяют в дисперсное облако. Таким образом, физические процессы описываются не для каждой частички в отдельности, а для объёма пространства, обладающего свойствами сплошной среды. Поэтому при моделировании многофазного течения облако частиц и несущая сплошная фаза взаимодействуют как взаимопроникающие сплошные среды.

Однако при таком подходе не учитываются в явном виде столкновения частиц друг с другом и, как следствие, напряжение внутри облака отсутствует. Для учёта взаимодействия частиц между собой в рамках Эйлерова подхода традиционно вводят дополнительные модели, например, модель кипящего слоя. Во FlowVision реализована простая модель расталкивая частиц, включающая в уравнении движения частиц дополнительное слагаемое с коэффициентами, редактируемыми в интерфейсе FlowVision.

Почему в дисперсном решателе используется Эйлеров подход?

Другой подход к моделированию частиц в сплошной среде - Лагранжев. Он предполагает решение большего числа уравнений для модельных частиц. Каждая модельная частица представляет некоторое (достаточно большое) число реальных частиц. Лагранжев солвер фиксирует перемещение модельных частиц с грани на грань каждой ячейки, через которую проходит траектория частицы. Лагранжев метод был реализован во FlowVision 2-го поколения. Но во FlowVision  3.xx.xx было принято решение реализовать Эйлеров метод, требующий меньше вычислительных ресурсов и меньше оперативной памяти. У обоих методов (Эйлерова и Лагранжева) есть свои преимущества и недостатки. Их обсуждение можно найти в гидродинамической литературе. 

Что умеет моделировать FlowVision с помощью частиц?

• Многофазные дисперсные течения: аэрозоли, порошки, эмульсии, суспензии
• Движение пузырьков газа в жидкости (с учётом изменения размера пузырьков)
• Испарение жидких капель 
• Горение угля и подобных веществ, которые разделяются на воду, кокс и золу
• Распыление струи форсункой (с учётом дробления и слития капель)
• Обледенение поверхности

Ограничения

1. Текущая реализация FlowVision не позволяет добавить в модель больше одной дисперсной фазы (моделируем только Частицы или только Каркас). 
2. FlowVision пока не моделирует фазовый переход превращения сплошной фазы в дисперсную. 

Помимо ограничений есть и возможности

1. Частицы могут участвовать в многофазном VOF взаимодействии: (частицы + сплошная #1) + сплошная #2.
2. Во FlowVision 3.12.02 добавлена модель конденсации частиц. Моделирование конденсации находится в стадии бета-тестирования, при возникновении сложностей в применении модели обращайтесь в службу технической поддержки, support@flowvision.ru.
3. Частицы совместимы с периодическими граничными условиями и скользящей поверхностью.

Дисперсные течения: шаг за шагом

Дисперсные течения - наиболее обширный и поэтому самый популярный класс дисперсных пользовательских задач. (Задачи дисперсного распада, обледенения и горения угля тоже пользуются успехом, но в меньшей степени). Туманы, аэрозоли, порошки, твёрдые примеси, суспензии (цементный раствор, апельсиновый сок) и эмульсии (битум, молоко) - все эти вещества окружают нас не только в промышленности, но и в повседневной жизни. Перейдём от теории к практике и добавим частицы в обучающий пример с ламинарным течением в трубе. Пусть теперь в трубе течет не вода, а взвесь воды и песка (SiO₂).

Вы можете скачать клиентскую часть проекта "Течение песка и воды в трубе", чтобы собственными глазами увидеть все настройки. Но далее мы всё равно обсудим самые важные из них.

• Количество размерных семейств в спектре
• Физические процессы в дисперсной фазе
• Коэффициент сопротивления облака частиц 
• Число Нуссельта
• Дисперсные настройки на ГУ 
• Многофазность Д
• Переменные в Постпроцессоре

Просто добавь частицы

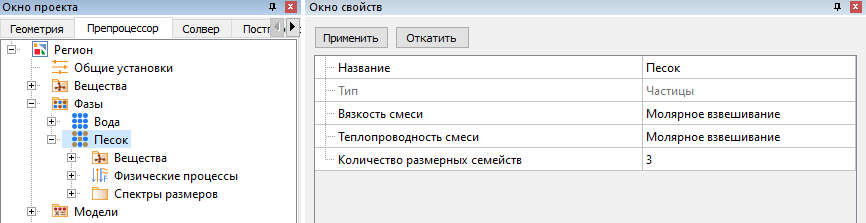
Начните моделирование дисперсных течений с сознания фазы "Частицы" и сразу переходите к ключевым настройкам: Частицы > Количество размерных семейств.

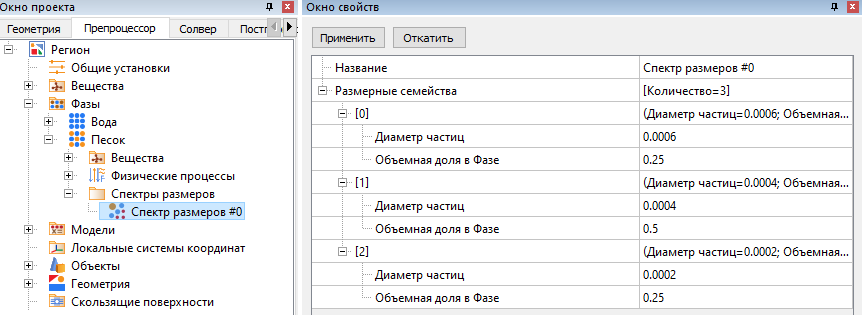
После создайте Спектр размеров, который будет состоять из трёх размерных семейств с разным диаметром. Безусловно, стоить помнить, что сумма объёмных долей всех семейств = 1.

В одной фазе можно задать максимум 100 различных размерных семейств 

Скорее всего вам и не потребуется больше. Ограничение на количество семейств связано с возможностями расчётных машин: для каждого (из 100!) размерных семейств выделяется определённый объём оперативной памяти, которая в современных реалиях не бесконечна. 

Физические процессы

Определим более подробно моделируемую задачу. Пусть на вход трубы подаётся горячий песок (Т = 50 °С) и холодная вода (Т = 0 °С) в соотношении 1:4. При этом можно выделить три семейства песчинок с размерами (d1 < d2 < d3) в соотношении 1:2:1. Смесь воды и песка, перемешиваясь, протекает по трубе и выходит из другого конца трубы. 

Для моделирование учитываем процессы: 

• Теплоперенос в дисперсной фазе (как часть процесса теплообмена между дисперсной средой и сплошной фазами)  > теплоперенос = конвекция и теплопроводность 
• Перенос частичек разного диаметра внутри дисперсной фазы > перенос фазы = конвекция и диффузия 
• Движение облака частиц в сплошной фазе > движение 

Коэффициент сопротивления частиц

Модель > Взаимодействие фаз > Сплошная - Частицы > Сd
Для расчёта коэффициента сопротивления частиц выберите одну из пяти моделей.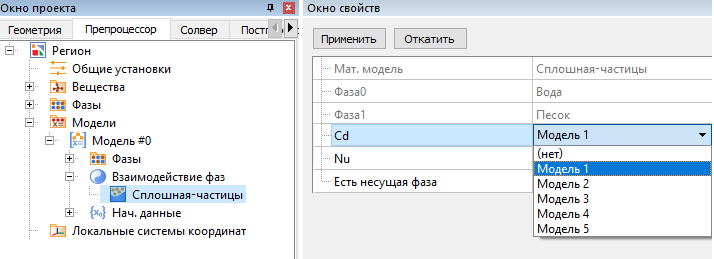 

Коэффициент сопротивления дисперсного облака (Cd) определяется средой, в которой оно протекает. Для сплошной среды (с числом Кнудсена, Kn < 0.001) обычно говорят о зависимости коэффициента сопротивления от числа Рейнольдса Re.

Параметры с индексом  "с" - это  параметры сплошной среды,  с индексом "d" - параметры дисперсной среды

 

Первый из учёных, кто предложил зависимость коэффициента сопротивления от числа Рейнольдса, был сэр Джордж Габриель Стокс. Выведенная им зависимость отлично согласуется с экспериментами для чисел Re < 0.1.

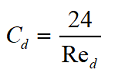• Модели 1, 2 близки к Стоксовому режиму, когда частицы обладают малой скоростью относительно общего потока.
  
  
• Модели 3, 4 разработаны на основе трудов (Ergun/Wen and Yu) и (Cheng) соответственно и позволяют расширить диапазон дисперсных числа Re < 3⋅10⁵. Эти модели хорошо работают при моделировании распыления частиц в неподвижном пространстве.
  
  
• Модель 5 используется при пузырьковом моделировании, подробнее об этом процессе читайте в следующей дисперсной статье.

Число Нуссельта 

Модель > Взаимодействие фаз > Сплошная - Частицы > Nu
Для расчёта числа Нуссельта частиц выберите одну из двух моделей.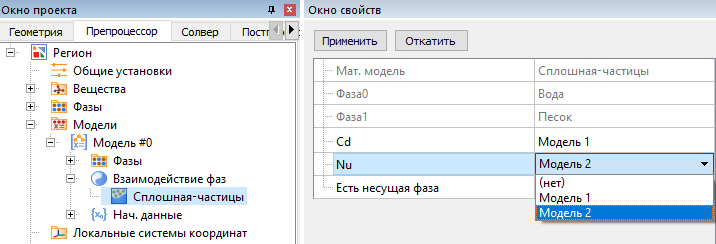 

Число Нуссельта (Nu) характеризует соотношение между интенсивностями теплообмена за счёт конвекции и за счёт теплопроводности и определяет тепловой поток: 

• Модель 1 более универсальная, и подходит для моделирования совместного движения частиц в потоке, так и движения частиц в неподвижном пространстве. 
• Модель 2  расщепляется на два выражения для расчёта на низких и высоких числах Re.

Дисперсные настройки на граничных условиях

Для заданных физических процессов на граничных условиях необходимо определить следующие дисперсные величины: 

• Объёма фазы (Песок)
• Температуры (дисп.) (Песок)
• Скорости (дисп.) (Песок) 

Вход (inlet)

На входе задаются значения из исходных данных. Значения объёма фазы ( = 1/5 = 0.2), температуры ( = 50 при T оп. = 273) и скорости ( = 1) нам известны.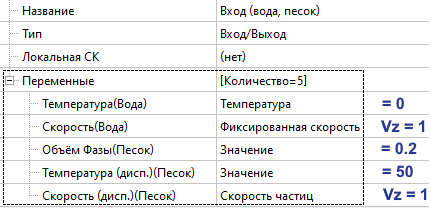 

При известном расходе частиц через ГУ можно задать либо объёмную скорость (V_d⋅φ_d) либо массовую скорость (ρ_d⋅V_d⋅φ_d)

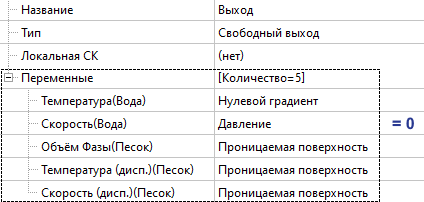
Выход (outlet)

На поверхности, соответствующей физическому выходу, для всех переменных дисперсной фазы задаём условие проницаемой поверхности, что обеспечивает невозмущённое течение дисперсной фазы. Условие проницаемой поверхности - это аналог условия нулевого градиента для сплошной фазы. Для воды также задаём невозмущённое вытекание среды через нулевое значение давления.

Если известен расход или параметры на выходе, то на выходном ГУ можно задавать и фиксированные значения дисперсных переменных 

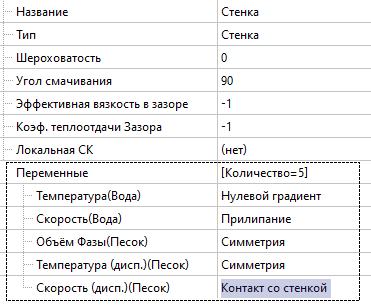
Поверхность трубы (wall) 

На стенке трубы скорость определяем через условие контакта со стенкой, внутри которого можно варьировать направление отскока частиц от стенки.

Если вы моделируете мембраны, то FV позволяет задать и условие проницаемой стенки: задайте значение объёма фазы, температуры и скорости (всё как на входном ГУ), а для сплошной фазы оставьте условия не протекания - стенки

Многофазность Д

Настройки дисперсной многофазности задаются на вкладке Солвер > Доп. настройки.   

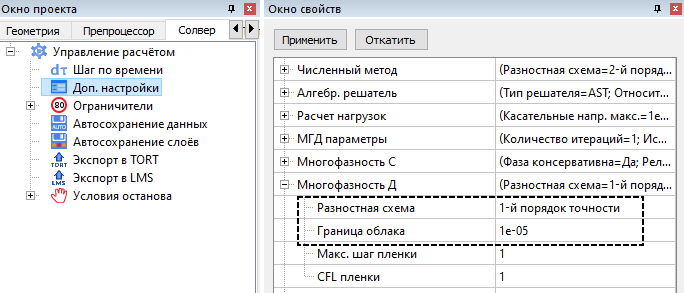Максимальный шаг плёнки и CFL плёнки задаются только при моделировании влажного режима обледенения. В этом контексте Разностная схема и Граница облака более универсальные дисперсные параметры. 

• Опытным путём было определено, что в текущей реализации FlowVision задание 1-го порядка точности разностной схемы позволяет получить более стабильное решение. 
  
• Граница облака определяет нижнюю границу для величины дисперсной фазы в ячейке. Если действительное значение фазы меньше границы облака, то частицы, находящиеся в этой ячейке, не участвуют в расчёте. По умолчанию значение границы облака = 1e-5.

ПостПроцессинг: дисперсные переменные

Полный список дисперсных переменных отображается при выборе категории Переменные фазы "Песок". Рассмотрим типовые из них:

• Концентрация [м^-3] - количество частиц в ячейке
• Объём фазы [-] - доля дисперсной фазы в ячейке
• Скорость (дисп.) [м/с] и Температура (дисп.) [K] относятся только к дисперсной фазе. Соответствующие переменные в сплошной фазе обозначаются Скорость и Температура

Принадлежность частиц к определённому размерному семейству фиксируется индексом в квадратных скобках - [0,1 или 2]

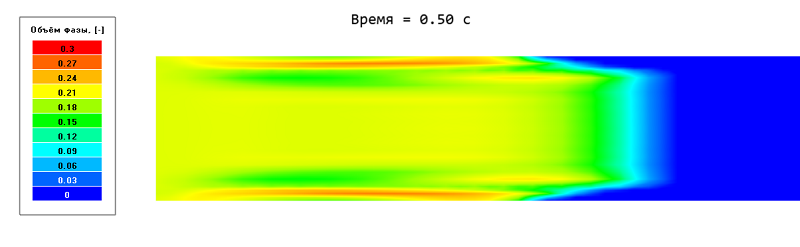
Например, объём фазы определяет суммарную долю дисперсной фазы, а объём фазы [1]  определяет только долю частиц 1-го семейства (с диаметром 0,0004 м). Отобразим  распределения песка вблизи входа в трубу. Для этого используем переменную фазы "Песок" > Объём фазы. 

То же самое, но кратко

1. Частицы - это не связанные между собой элементы среды: жидкой (капли), твёрдой (песчинки, пылинки, снежинки) или газообразной (пузыри), разделённые сплошной средой (жидкой или газообразной), называемой несущей фазой. В зависимости от комбинации дисперсной и сплошной сред образуются различные привычные нам дисперсные системы: пыль в воздухе, пузыри в шампанском, твёрдые частицы в жидкости (суспензии), капли в жидкости (эмульсии).
   
   
2. При моделировании частиц во FlowVision применяется Эйлеров подход, позволяющий оптимизировать использование расчётных ресурсов в многофазном расчёте за счёт уменьшения числа решаемых уравнений и оперативной памяти компьютера.
   
   
3. На данный момент во FlowVision моделируют: 

• • Многофазные дисперсные течения: аэрозоли, порошки, эмульсии, суспензии
  • Движение пузырьков газа в жидкости (с учётом изменения размера пузырьков)
  • Испарение жидких капель 
  • Горение угля и подобных веществ, которые разделяются на воду, кокс и золу
  • Распыление струи форсункой (с учётом дробления и слития капель)
  • Обледенение поверхности

4.  Ключевые этапы в создании проекта для моделирования дисперсного течения это: 

• • Определение количества размерных семейств в спектре частиц
  • Задание физических процессов в дисперсной фазе
  • Выбор модели для коэффициента сопротивления облака частиц 
  • Выбор модели для числа Нуссельта
  • Дисперсные настройки на ГУ 
  • Дисперсные настройки для продвинутых пользователей
  • Выбор переменных для отображения в ПостПроцессоре